题目内容
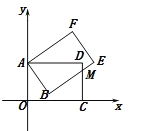
【题目】将两个全等的矩形AOCD和矩形ABEF放置在如图所示的平面直角坐标系中,已知A(0,5),边BE交边CD于M,且ME=2,CM=4.
(1)求AD的长;
(2)求经过A、B、D三点的抛物线解析式.
【答案】(1)7;(2)![]() .
.
【解析】
(1)连接AM,设OC=AD=m,得出BM=m-2,DM=1,利用勾股定理得出AB2+BM2=AD2+DM2,依此列出方程52+(m-2)2=m2+12,解方程即可;
(2)过点B作x轴的平行线GH,交OA、CD于G、H,由(1)可知AB=BM=5,设G(0,n),根据AAS可证△ABG≌△BMH,得出GB=MH=4-n,BH=AG=5-n,由GH=GB+BH=9-2n,GH=OC=7,得出n=1,所以B(3,1),又因为D(7,5),A(0,5),利用待定系数法即可求出经过A、B、D三点的抛物线解析式.
解:(1)如图1,连接AM,
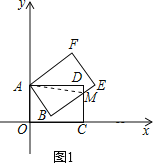
设OC=AD=m,
根据已知条件可知,AB=CD=OA=5,BE=OC=m,
所以,![]() ,DM=1,
,DM=1,
∵四边形AOCD和四边形ABEF是全等的矩形
根据勾股定理,可得:![]() ,
,
∴所以![]() ,
,
解得m=7,即AD=7;
(2)如图2,过点B作x轴的平行线GH,交OA、CD于G、H,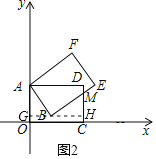
由(1)可知![]() ,则有
,则有![]() ,
,
∵![]() ,四边形AOCD和四边形ABEF是全等的矩形
,四边形AOCD和四边形ABEF是全等的矩形
∴![]() ,
,![]() ,
,![]()
∴![]()
∴![]() (AAS),
(AAS),
设G(0,n),则HC=OG=n,所以GB=MH=4-n,BH=AG=5-n,
∵![]() ,
,![]() ,
,
∴![]() ,即
,即![]() ,
,
∴B点的坐标为(3,1),
又∵D点坐标为(7,5),A点坐标为(0,5),
设经过A、B、D三点的抛物线解析式为y=ax2+bx+c,将A,B,D三点坐标代入得: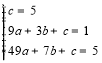 ,解得
,解得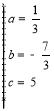 ,
,
∴抛物线为![]() .
.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目