题目内容
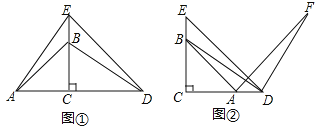
【题目】已知,平面直角坐标系中,A(0,4) ,B (b,0) (-4<b<0),将线段AB绕点A逆时针旋转90°得到线段AC,连接BC.
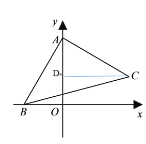
(1)如图1,直接写出C点的坐标: ;(用b表示)
(2)如图2,取线段BC的中点D,在x轴取一点E使∠DEB=45°,作CF⊥x轴于点F.
①求证:EF=OB;
②如图3,连接AE,作DH∥y轴交AE于点H,当OE=EF时,求线段DH的长度.



图1 图2 图3
【答案】(1) ①(4,b+4);(2) ①见解析;②1.
【解析】
(1)作CD⊥y轴,易知△ABO≌△CAD,即可求出C点坐标;
(2)连AD、OD作DP⊥OD交y轴于P,易证△DBO≌△DAP,得出PO=OE,再根据OA=OF即可证明EF=OB;②连结OD、AD,作直线DH交x轴于M,作AN⊥DH于N
DM⊥EF,则EM=MD=MF=1,证得△BDM≌△DAN,求得NH=HM=2,DH=HM-DM=1
(1)作CD⊥y轴,
∵将线段AB绕点A逆时针旋转90°得到线段AC,
∴AB=AC,∠BAO+∠DAC=∠BAC=90°,
又∠BAO+∠ABO=90°,
∴∠ABO=∠DAC,
又∠AOB=∠CDA=90°,
∴△ABO≌△CAD,
∵A(0,4) ,B (b,0) ,
∴AO=4,BO=-b
∴CD=AO=4,DO=AO-AD=AO-BO=4+b,
∴C点坐标为(4,b+4);
(2)①连AD、OD作DP⊥OD交y轴于P
∴∠DOA=∠DEB
由(1)得AB=AC,故AD⊥BC,AD=BD
∴∠ADP+∠PDB=90°,
∵∠PDB+∠BDO=90°,
∴∠ADP=∠BDO
∴△DBO≌△DAP
得BO=AP,∠DPO=∠DOP=45°
则PD的延长线过点E
∴PO=OE
又OA=OF=4,则EF=AP=BO.
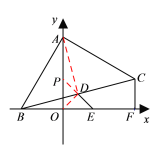
②∵OE=EF=OB=![]() .
.
连结OD、AD,作直线DH交x轴于M,作AN⊥DH于N
DM⊥EF,则EM=MD=MF=1
又AD=BD,∠BMD=∠DNA
∴△BDM≌△DAN
BM=DN=2+1=3
∴AN=DM=ME
又∠ANH=∠EMH=90°,∠AHN=∠EHM,
∴△AHN≌△EHM
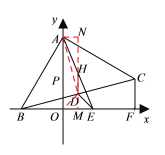
NH=HM=![]() =2
=2
则DH=HM-DM=2-1=1.

 名校课堂系列答案
名校课堂系列答案【题目】体育老师为了解本校九年级女生1分钟“仰卧起坐”体育测试项目的达标情况,从该校九年级136名女生中,随机抽取了20名女生,进行了1分钟仰卧起坐测试,获得数据如下:
收集数据:抽取20名女生的1分钟仰卧起坐测试成绩(个)如下:
38 46 42 52 55 43 59 46 25 38
35 45 51 48 57 49 47 53 58 49
(1)整理、描述数据:请你按如下分组整理、描述样本数据,把下列表格补充完整:
范围 | 25≤x≤29 | 30≤x≤34 | 35≤x≤39 | 40≤x≤44 | 45≤x≤49 | 50≤x≤54 | 55≤x≤59 |
人数 |
|
|
|
|
|
|
|
(说明:每分钟仰卧起坐个数达到49个及以上时在中考体育测试中可以得到满分)
(2)分析数据:样本数据的平均数、中位数、满分率如下表所示:
平均数 | 中位数 | 满分率 |
46.8 | 47.5 | 45% |
得出结论:①估计该校九年级女生在中考体育测试中1分钟“仰卧起坐”项目可以得到满分的人数为 ;
②该中心所在区县的九年级女生的1分钟“仰卧起坐”总体测试成绩如下:
平均数 | 中位数 | 满分率 |
45.3 | 49 | 51.2% |
请你结合该校样本测试成绩和该区县总体测试成绩,为该校九年级女生的1分钟“仰卧起坐”达标情况做一下评估,并提出相应建议.