��Ŀ����
����Ŀ�������¹ڷ��ײ�����Űȫ�������� KN95 �ȷ����Ϳ��ֳ����������人��ijѧУ������һ�����֣���֪ 3 �� A �Ϳ��ֺ� 2 �� B �Ϳ��ֹ��� 95 Ԫ��10 �� A �Ϳ��ֺ� 5 �� B �Ϳ��ֹ��� 250 Ԫ��
(1)��һ�� A �Ϳ��ֺ�һ�� B �Ϳ��ֵ��ۼ۸��Ƕ���Ԫ��
(2)ѧУ�������������ͺŵĿ��ֹ� 500 �������ø���ҩ��Կ��ּ۸���е��������� A �Ϳ����ۼ۱�ԭ����� 7 Ԫ��B �Ϳ��ְ�ԭ�۾����۳��ۣ���ѧУ�˴ι������ֿ��ֵ��ܷ��ò����� 10000 Ԫ���ұ�֤����� B �Ϳ�������������135 ��������Ƴ���ʡǮ�Ĺ�������������ͷ��ã�
���𰸡���1��A�Ϳ���ÿ��5Ԫ��B�Ϳ���ÿ��40Ԫ����2������A�Ϳ���365����B�Ϳ���135������ͷ���Ϊ9510Ԫ��
��������
��1����һ�� A �Ϳ���xԪ��һ�� B �Ϳ���yԪ������������ϵ�г���Ԫһ�η������ɣ�
��2���蹺��B�Ϳ���a��������ΪWԪ�������һ�� A �Ϳ��ֺ�һ�� B �Ϳ������ڵ��ۼۣ����ݲ��ȹ�ϵ�г�����ʽ�����a��ȡֵ��Χ���ú���a�Ĵ���ʽ��ʾ��W������һ�κ����������Խ���Ա�����ȡֵ��Χ���ɽ��
��1����һ�� A �Ϳ���xԪ��һ�� B �Ϳ���yԪ����������ã�
![]()
��ã�![]()
��һ��A�Ϳ����ۼ���5Ԫ��һ��B�Ϳ���40Ԫ��
��2���蹺��B�Ϳ���a��������ΪWԪ����
һ��A�Ϳ������ۼۣ�5+7=12Ԫ
һ��B�Ϳ������ۼۣ�40��0.95=38Ԫ
��������ã�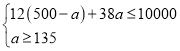
��ã�![]()
W=![]()
W��a��һ�κ�������W��a����������ʵ�a=135ʱW��С��
W��С=26��135+600=9510Ԫ
��ʱ����A�Ϳ���365����B�Ϳ���135����
����ʡǮ�Ĺ���Ϊ������A�Ϳ���365����B�Ϳ���135������ͷ���Ϊ9510Ԫ��