题目内容
【题目】如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是45°,向前走9m到达B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°.
(1)求∠BPQ的度数;
(2)求该电线杆PQ的高度.(结果保留根号)
【答案】
(1)解:延长PQ交直线AB于点E,如图所示:
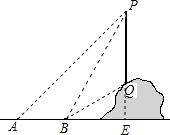
∠BPQ=90°﹣60°=30°;
(2)解:设PE=x米.
在Rt△APE中,∠A=45°,
则AE=PE=x米;
∵∠PBE=60°,
∴∠BPE=30°,
在Rt△BPE中,BE= ![]() PE=
PE= ![]() x米,
x米,
∵AB=AE﹣BE=9米,
则x﹣ ![]() x=9,
x=9,
解得:x= ![]() .
.
则BE= ![]() 米.
米.
在直角△BEQ中,QE= ![]() BE=
BE= ![]() 米.
米.
∴PQ=PE﹣QE= ![]() ﹣
﹣ ![]() =9+3
=9+3 ![]() (米).
(米).
答:电线杆PQ的高度为(9+3 ![]() )米.
)米.
【解析】(1)延长PQ交直线AB于点E,根据直角三角形两锐角互余求得即可。
(2)设PE=x米,在Rt△APE和Rt△BPE中,根据三角函数利用x表示出AE和BE,根据AB=AE-BE即可列出方程求得x的值,再在Rt△BQE中利用解直角三角形求得QE的长,即可求出PQ的长度。
【考点精析】本题主要考查了特殊角的三角函数值和解直角三角形的相关知识点,需要掌握分母口诀:30度、45度、60度的正弦值、余弦值的分母都是2,30度、45度、60度的正切值、余切值的分母都是3,分子口诀:“123,321,三九二十七”;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)才能正确解答此题.

练习册系列答案
相关题目





