题目内容
 已知如图,Rt△ABC中,∠ACB=90゜,D是AB上一点,BD=BC,过D作AB的垂线交AC于E,连CD交BE于F,求证:
已知如图,Rt△ABC中,∠ACB=90゜,D是AB上一点,BD=BC,过D作AB的垂线交AC于E,连CD交BE于F,求证:(1)CE=DE;
(2)BE⊥CD;
(3)∠ABE=∠ACD.
分析:(1)利用HL定理证明△BCE≌△BDE可得CE=DE;
(2)根据全等三角形的性质可得EC=ED,BC=BD,进而得到BE垂直平分CD,即可得到BE⊥CD;
(3)根据垂直平分线的性质可得∠ECD=∠EDC,再根据同角的余角相等可得∠EDC=∠DBE,进而得到∠ACD=∠ABE.
(2)根据全等三角形的性质可得EC=ED,BC=BD,进而得到BE垂直平分CD,即可得到BE⊥CD;
(3)根据垂直平分线的性质可得∠ECD=∠EDC,再根据同角的余角相等可得∠EDC=∠DBE,进而得到∠ACD=∠ABE.
解答:证明:(1)∵ED⊥AB,
∴∠EDB=90°,
在Rt△BCE和Rt△BDE中,
,
∴△BCE≌△BDE(HL),
∴CE=DE;
(2)∵△BCE≌△BDE,
∴EC=ED,BC=BD,
∴BE垂直平分CD,
∴BE⊥CD;
(3)∵BE垂直平分CD,
∴∠ECD=∠EDC,∠DFB=90°,
∵∠EDB=90°,
∴∠EDF+∠FDB=90°,
∠FDB+∠DBF=90°,
∴∠EDC=∠DBE,
∴∠ACD=∠ABE.
∴∠EDB=90°,
在Rt△BCE和Rt△BDE中,
|
∴△BCE≌△BDE(HL),
∴CE=DE;
(2)∵△BCE≌△BDE,
∴EC=ED,BC=BD,
∴BE垂直平分CD,
∴BE⊥CD;

(3)∵BE垂直平分CD,
∴∠ECD=∠EDC,∠DFB=90°,
∵∠EDB=90°,
∴∠EDF+∠FDB=90°,
∠FDB+∠DBF=90°,
∴∠EDC=∠DBE,
∴∠ACD=∠ABE.
点评:此题主要考查了全等三角形的判定与性质,以及线段垂直平分线的性质,关键是掌握全等三角形的判定定理.

练习册系列答案
相关题目
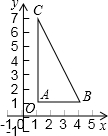 AB=3,AC=6.
AB=3,AC=6. (1997•重庆)已知如图,Rt△ABC中,∠C=90°,tan∠DAC=
(1997•重庆)已知如图,Rt△ABC中,∠C=90°,tan∠DAC= 的图象与直线BC有交点,求k的最大正整数.
的图象与直线BC有交点,求k的最大正整数.

 (k≠0)的图象与直线BC有交点,求k的最大正整数。
(k≠0)的图象与直线BC有交点,求k的最大正整数。