题目内容
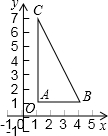
已知如图,Rt△ABC位于第一象限,A点的坐标为(1,1),两条直角边AB、AC分别平行于x轴、y轴,且AB=3,AC=6.(1)求直线BC的方程;
(2)若反比例函数
 的图象与直线BC有交点,求k的最大正整数.
的图象与直线BC有交点,求k的最大正整数.
【答案】分析:(1)由图求出B、C点坐标,利用待定系数法求出函数解析式;
(2)将反比例函数 代入直线BC的解析式,转化为二次函数根的判别式解答.
代入直线BC的解析式,转化为二次函数根的判别式解答.
解答:解:(1)∵A点的坐标为(1,1),两条直角边AB、AC分别平行于x轴、y轴,
AB=3,AC=6,
∴B(4,1),C(1,7).
∴直线AB的方程为:y=-2x+9;
(2)把 代入y=-2x+9整理得2x2-9x+k=0.
代入y=-2x+9整理得2x2-9x+k=0.
由于△=b2-4ac=81-8k≥0,解得: .
.
∴k的最大正整数为10.
点评:此题考查了用待定系数法求函数解析式,要利用图形的特点,求出相应点的坐标,进而求出函数解析式,解答此题还要注意转化思想的应用.
(2)将反比例函数
 代入直线BC的解析式,转化为二次函数根的判别式解答.
代入直线BC的解析式,转化为二次函数根的判别式解答.解答:解:(1)∵A点的坐标为(1,1),两条直角边AB、AC分别平行于x轴、y轴,
AB=3,AC=6,
∴B(4,1),C(1,7).
∴直线AB的方程为:y=-2x+9;
(2)把
 代入y=-2x+9整理得2x2-9x+k=0.
代入y=-2x+9整理得2x2-9x+k=0.由于△=b2-4ac=81-8k≥0,解得:
 .
.∴k的最大正整数为10.
点评:此题考查了用待定系数法求函数解析式,要利用图形的特点,求出相应点的坐标,进而求出函数解析式,解答此题还要注意转化思想的应用.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
 AB=3,AC=6.
AB=3,AC=6. (1997•重庆)已知如图,Rt△ABC中,∠C=90°,tan∠DAC=
(1997•重庆)已知如图,Rt△ABC中,∠C=90°,tan∠DAC= 已知如图,Rt△ABC中,∠ACB=90゜,D是AB上一点,BD=BC,过D作AB的垂线交AC于E,连CD交BE于F,求证:
已知如图,Rt△ABC中,∠ACB=90゜,D是AB上一点,BD=BC,过D作AB的垂线交AC于E,连CD交BE于F,求证:
 (k≠0)的图象与直线BC有交点,求k的最大正整数。
(k≠0)的图象与直线BC有交点,求k的最大正整数。