Question

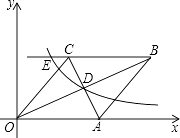
【题目】如图，△ABC的两条高AD，BE交于点F，∠ABC＝45°，∠BAC＝60°．

（1）求证：DF＝DC；

（2）连接CF，求证：AB＝AC+CF．

Answer 1

【答案】（1）证明见解析；（2）证明见解析

【解析】

（1）欲证明DF=DC，只要证明△BDF≌△ADC即可解决问题；

（2）延长FE到K，使得EK=EF，连接CF．想办法证明CF=FK，BK=BA即可解决问题.

（1）∵AD⊥BC，

∴∠ADB＝∠ADC＝90°，

∵∠ABC＝45°，

∴∠DBA＝∠DAB＝45°，

∴BD＝DA，

∵BE⊥AC，

∴∠BEC＝90°，

∴∠DAC+∠C＝90°，∠CBE+∠C＝90°，

∴∠DAC＝∠DBF，

在△BDF和△ADC中，

，

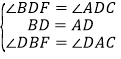∴△BDF≌△ADC（ASA），

∴DF＝DC;

（2）延长FE到K，使得EK＝EF，连接CF，

∵∠BAC＝60°，∠ABC＝45°，

∴∠ACB＝180°﹣60°﹣45°＝75°，

∵DF＝DC，∠FDC＝90°，

∴∠FCD＝∠DFC＝45°，

∴∠ECF＝30°，

∵∠CEF＝90°，

∴CF＝2EF，

∵FK＝2EF，

∴CF＝FK，

∵AE⊥FK，EF＝EK，

∴AF＝AK，

∴∠K＝∠AFE，∠EAF＝∠EAF，

∵∠ADC＝90°，∠ACD＝75°，

∴∠DAC＝15°，

∴∠EAF＝∠EAK＝15°，

∴∠K＝90°﹣15°＝75°，

∴∠BAK＝∠BAD+∠DAK＝75°，

∴∠BAK＝∠K，

∴BA＝BK，

∴AB＝BF+FK＝BF+CF．