��Ŀ����
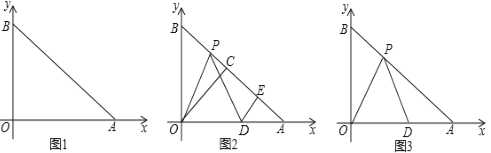
����Ŀ������ABCD�У�BC=3��AB=8��E��FΪAB��CD���ϵ��е㣬��ͼ1��A��ԭ�㴦����B��y���������ϣ���C�ڵ�һ���ޣ�����A��ԭ���������x��������ÿ��1����λ���ȵ��ٶ��˶������B��֮��y���»�������������ABCD��ƽ���ϻ�������ͼ2�����˶�ʱ���ʾΪt�룬��B����ԭ��ʱֹͣ�˶���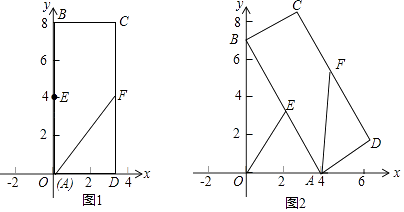
��1����t=0ʱ�����F�����꼰FA�ij��ȣ�
��2����t=4ʱ����OE�ij�����BAO�Ĵ�С��
��3�����t=0��t=4��һʱ�ε�E�˶�·�ߵij���
��4�����Ե�FΪԲ�ģ�FAΪ�뾶��Բ������������ʱ����t��ֵ��
���𰸡�
��1���⣺��t=0ʱ��
��AB=CD=8��FΪCD�е㣬
��DF=4��
��F��3��4����
��AF=5
��2���⣺��t=4ʱ��OA=4��
��Rt��ABO�У�AB=8����AOB=90�㣬��E��AB���е㣬
���ABO=30�㣬OE=4��
���BAO=60��
��3���⣺��t=0��t=4��һʱ�Σ���E�˶�·������OΪԲ�ģ�OEΪ�뾶Բ�Ľ���30���һ�λ���
������OE=OE1=4����E1OE=90�㩁60��=30�㣬��
���E�˶�·�ߵij�Ϊ ![]() =
= ![]() �У�
�У� 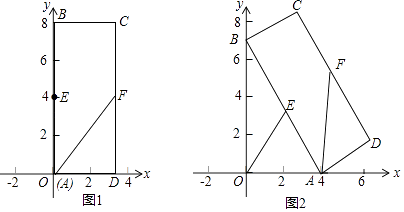
��4���⣺��Rt��ADF�У�FD2+AD2=AF2��
��AF= ![]() =5��
=5��
����AO=t1ʱ����F��x�����У���AΪ�е㣬
��FA��OA��
���OAB+��FAB=90�㣬
�ߡ�FAD+��FAB=90�㣬
���BAO=��FAD��
�ߡ�BOA=��D=90�㣬
��Rt��FAE��Rt��ABO��
�� ![]() ��
��
�� ![]() ��
��
��t1= ![]() ��
��
����AO=t2ʱ����F��y�����У�BΪ�е㣬ͬ���ɵã�t2= ![]() ��
��
�������������Ե�FΪԲ�ģ�FAΪ�뾶��Բ������������ʱ��t��ֵΪ ![]() ��
�� ![]() ��
��
����������1��FΪCD���ϵ��е㣬���DF�ó��������ó���F�����꼴�ɵó�AF��
��2������ֱ�������ε����ʣ�ֱ��������б���ϵ����ߵ���б�ߵ�һ�룬֤�á�AOE�ǵȱ������Σ����ɵó����ۡ�
��3�����жϳ���E�˶���·����һ���������û�����ʽ���ɵó����ۣ�
��4�����������������AO=t1ʱ����F��x�����У���AΪ�е㣻����AO=t2ʱ����F��y�����У�BΪ�е㣬�������������ε����ʽ���������⼴�ɣ�
�����㾫����������Ĺؼ���������ֱ��������б���ϵ����ߵ����֪ʶ������ֱ��������б���ϵ����ߵ���б�ߵ�һ�룬�Լ��Թ��ɶ����ĸ�������⣬�˽�ֱ����������ֱ�DZ�a��b��ƽ���͵���б��c��ƽ��,��;a2+b2=c2��