题目内容
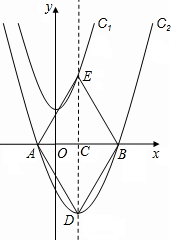
已知,抛物线y=ax2-2ax与x轴交于A、B两点(点A在点B的右侧),且抛物线与直线y=-2 ax-1的交点恰为抛物线的顶点C.
ax-1的交点恰为抛物线的顶点C.
(1)求a的值;
(2)如果直线y=-x+b(
≤b≤
)与x轴交于点D,与线段BC交于点E,求△CDE面积的最大值;
(3)在(2)的结论下,在x轴下方,是否存在点F,使△BDF与△BCD相似?如果存在,请求出点F的坐标;不存在,请说明理由.
 ax-1的交点恰为抛物线的顶点C.
ax-1的交点恰为抛物线的顶点C.(1)求a的值;
(2)如果直线y=-x+b(
| 2 |
| 3 |
(3)在(2)的结论下,在x轴下方,是否存在点F,使△BDF与△BCD相似?如果存在,请求出点F的坐标;不存在,请说明理由.
(1)∵y=ax2-2ax=ax(x-2),
又∵抛物线y=ax2-2ax与x轴交于A、B两点(点A在点B的右侧),
∴A(2,0),B(0,0),顶点C(1,-a),
∵抛物线与直线y=-2ax-1的交点恰为抛物线的顶点C,
∴-2a-1=-a,
解得:a=-1.
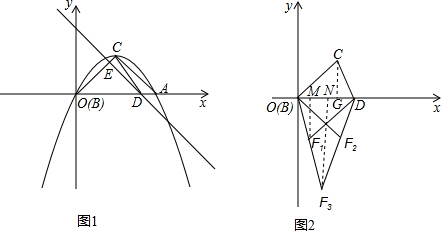 (2)如图1,由(1)得直线BC的解析式为y=x,
(2)如图1,由(1)得直线BC的解析式为y=x,
∵直线y=-x+b(
≤b≤
)与x轴交于点D,与线段BC交于点E,
∴D(b,0),E(
,
),
∴S△CDE=S△CBD-S△BDE=
×b×1-
×b×
=-
(b-1)2+
,
∵当b>1时,s随着b的增大而减小,
∵
≤b≤
,
∴当b=
时,△CDE面积最大,
最大值为:-
(
-1)2+
=
.
(3)如图2,△BCD中,BC=BD=
,∠CBD=45°,
在x轴下方存在点F,使△BDF与△BCD全等,即△BDF与△BCD相似,
∴F2(1,-1),
过点F1作F1M⊥OD于M,
∵DF1=OD=OC=
,∠ODF1=∠CBD=45°,
∴F1M=DM=1,
∴F1(
-1,-1),
过F3N⊥BD于N,过点C作CG⊥BD于G,
∴△CGD∽△F3ON,
∴CG:F3N=GD:BG,
∵GD=
-1,CG=1,BG=
,
∴
=
,
∴F3G=1+
,
∴F3(
,-1-
).
∴存在点F1(
-1,-1),F2(1,-1),F3(
,-1-
),使△BDF与△BCD相似.
又∵抛物线y=ax2-2ax与x轴交于A、B两点(点A在点B的右侧),
∴A(2,0),B(0,0),顶点C(1,-a),
∵抛物线与直线y=-2ax-1的交点恰为抛物线的顶点C,
∴-2a-1=-a,
解得:a=-1.
 (2)如图1,由(1)得直线BC的解析式为y=x,
(2)如图1,由(1)得直线BC的解析式为y=x,∵直线y=-x+b(
| 2 |
| 3 |
∴D(b,0),E(
| b |
| 2 |
| b |
| 2 |
∴S△CDE=S△CBD-S△BDE=
| 1 |
| 2 |
| 1 |
| 2 |
| b |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
∵当b>1时,s随着b的增大而减小,
∵
| 2 |
| 3 |
∴当b=
| 2 |
最大值为:-
| 1 |
| 4 |
| 2 |
| 1 |
| 4 |
| ||
| 2 |
(3)如图2,△BCD中,BC=BD=
| 2 |
在x轴下方存在点F,使△BDF与△BCD全等,即△BDF与△BCD相似,
∴F2(1,-1),
过点F1作F1M⊥OD于M,
∵DF1=OD=OC=
| 2 |
∴F1M=DM=1,
∴F1(
| 2 |
过F3N⊥BD于N,过点C作CG⊥BD于G,
∴△CGD∽△F3ON,
∴CG:F3N=GD:BG,
∵GD=
| 2 |
| ||
| 2 |
∴
| ||||
|
| 1 |
| F3G |
∴F3G=1+
| ||
| 2 |
∴F3(
| ||
| 2 |
| ||
| 2 |
∴存在点F1(
| 2 |
| ||
| 2 |
| ||
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

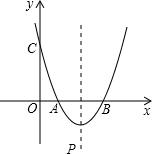 物线的顶点,若m-n=-2,m•n=3.
物线的顶点,若m-n=-2,m•n=3. ,求出点P的坐标,并求出梯形的面积;若不存在,请说明理由.
,求出点P的坐标,并求出梯形的面积;若不存在,请说明理由.