题目内容
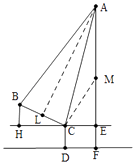
【题目】如图,分别是吊车在吊一物品时的示意图,已知吊车底盘CD的高度为2米,支架BC的长为4米,且与地面成30°角,吊绳AB与支架BC的夹角为75°,吊臂AC与地面成75°角. 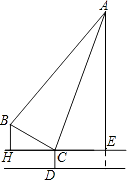
(1)求证:AB=AC
(2)求吊车的吊臂顶端A点距地面的高度是多少米?(保留根号)
【答案】
(1)证明:如图,∵∠BCH=30°,∠ACE=75°,
∴∠ACB=180°﹣∠BCH﹣∠ACE=75°,
∵∠ABC=75°,
∴∠ABC=∠BCA,
∴AB=AC
(2)解:作AL⊥BC于L,在AE上截取一点M,使得AM=MC.
在△ACL和△ACE中,
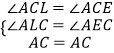 ,
,
∴△ACL≌△ACE,
∴CL=CE,
∵AB=AC,AL⊥BC,BC=4,
∴BL=CL=CE=2,
∵MA=MC,
∴∠MAC=∠MCA=90°﹣∠ACE=15°,
∴∠CME=30°,
∴CM=AM=2CE=4,ME=2 ![]() ,
,
∴AE=AM+ME=4+2 ![]() ,
,
∴AF=AE+EF=4+2 ![]() +2=6+2
+2=6+2 ![]() .
.
吊车的吊臂顶端A点距地面的高度是(6+2 ![]() )米.
)米.
【解析】(1)欲证明AB=AC,只要证明∠ABC=∠BCA即可.(2)作AL⊥BC于L,在AE上截取一点M,使得AM=MC.首先证明△ACL≌△ACE,得到CL=CE=2,只要证明∠CME=30°,求出CM,ME即可解决问题.

 考前必练系列答案
考前必练系列答案【题目】为了美化学习环境,加强校园绿化建设,某校计划用不多于5200元的资金购买A、B两种树苗共60棵(可以是同一种树苗),加强校园绿化建设.若购买A种树苗x棵,所需总资金为y元,A、B两种树苗的相关信息如表:
项目 | 单价(元/棵) | 成活率 |
A | 100 | 98% |
B | 60 | 90% |
(1)求y与x之间的函数关系式;
(2)若要使得所购买树苗的成活率不低于95%,有几种选购方案?所用的资金分别是多少?