题目内容
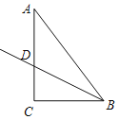
【题目】如图,在△ABC中,∠ACB=α(90°<α<180°),将△ABC绕着点A逆时针旋转2β(0°<β<90°)后得△AED,其中点E、D分别和点B、C对应,联结CD,如果CD⊥ED,请写出一个关于α与β的等量关系的式子_____.
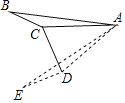
【答案】α+β=180°
【解析】
本题考查的是旋转与等腰三角形,做辅助线AF⊥CD,由旋转可得∠ADE=∠ACB=![]() ,再用含有字母
,再用含有字母![]() 的式子表示出∠ADC与∠DAF,利用三角形内角和即可倒出
的式子表示出∠ADC与∠DAF,利用三角形内角和即可倒出![]() 的关系
的关系
如图,过A作AF⊥CD,
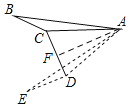
由旋转可得,∠ADE=∠ACB=α,
∵CD⊥DE,
∴∠ADC=α﹣90°,
由旋转可得,AC=AD,∠CAD=2β,
∴∠DAF=β,
∴Rt△ADF中,∠DAF+∠ADF=90°,即β+α﹣90°=90°,
∴α+β=180°.
故答案为:α+β=180°.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目