题目内容
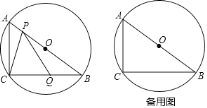
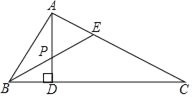
【题目】如图,在△ABC 中,点P是AC边上的一点,过点P作与BC平行的直线PQ,交AB于点Q,点D在线段 BC上,连接AD交线段PQ于点E,且![]() ,点G在BC延长线上,∠ACG的平分线交直线PQ于点F.
,点G在BC延长线上,∠ACG的平分线交直线PQ于点F.

(1)求证:PC=PE;
(2)当P是边AC的中点时,求证:四边形AECF是矩形.
【答案】(1)见解析;(2)见解析
【解析】
(1)根据相似三角形的性质得出![]() ,等量代换得到
,等量代换得到![]() ,推出
,推出![]() ,于是得出结论;
,于是得出结论;
(2)根据平行线的性质得到∠PFC=∠FCG,根据角平分线的性质得到∠PCF=∠FCG,等量代换得到∠PFC=∠FCG,根据等腰三角形的性质得到PF=PC,得到PF=PE,由已知条件得到AP=CP,推出四边形AECF是平行四边形,再证得∠ECF=90°,于是得出结论.
(1)证明:∵PQ∥BC,
∴△AQE∽△ABD,△AEP∽△ADC,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴PC=PE;
(2)∵PF∥DG,
∴∠PFC=∠FCG,
∵CF平分∠PCG,
∴∠PCF=∠FCG,
∴∠PFC=∠FCG,
∴PF=PC,
∴PF=PE,
∵P是边AC的中点,
∴AP=CP,
∴四边形AECF是平行四边形,
∵PQ∥CD,
∴∠PEC=∠DCE,
∴∠PCE=∠DCE,
∴![]() ,
,
∴∠ECF=90°,
∴平行四边形AECF是矩形.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目