题目内容
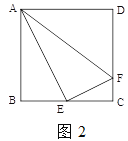
【题目】如图,![]() 中,
中,![]() 且
且![]() 是
是![]() 的中点
的中点
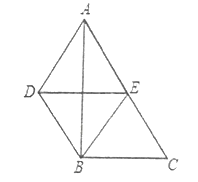
(1)求证:四边形![]() 是平行四边形。
是平行四边形。
(2)求证:四边形![]() 是菱形。
是菱形。
(3)如果![]() 时,求四边形ADBE的面积
时,求四边形ADBE的面积
(4)当![]() 度时,四边形
度时,四边形![]() 是正方形(不证明)
是正方形(不证明)
【答案】(1)见解析;(2)见解析;(3)24;(4)45.
【解析】
(1)推出CE=BD,CE∥BD,可证四边形![]() 是平行四边形;
是平行四边形;
(2)求出BDF=AE,BD∥AE,得出平行四边形ADBE,根据DE∥BC,∠ABC=90°推出DE⊥AB,根据菱形的判定推出即可;
(3)由四边形BDEC是平行四边形,可得DE=BC=6,然后根据菱形的面积公式求解即可;
(4)当![]() 45度时,可证△ABC是等腰直角三角形,从而AB=BC=DE,可证四边形
45度时,可证△ABC是等腰直角三角形,从而AB=BC=DE,可证四边形![]() 是正方形.
是正方形.
(1)证明:∵E是AC的中点,
∴CE=AE=![]() AC,
AC,
∵DB=![]() AC,
AC,
∵BD=CE,
∵BD∥AC,
∴BD∥CE,
∴四边形BDEC是平行四边形,
∴DE∥BC.
(2)证明:∵DE∥BC,∠ABC=90°,
∴DE⊥AB,
∵AE=![]() AC,DB=
AC,DB=![]() AC,BD∥AC,
AC,BD∥AC,
∴BD=AE,BD∥AE,
∴四边形ADBE是平行四边形,
∴平行四边形ADBE是菱形;
(3)∵四边形BDEC是平行四边形,
∴DE=BC=6.
∵四边形ADBE是菱形,
∴四边形ADBE面积=![]() ;
;
(4)当![]() 45度时,四边形
45度时,四边形![]() 是正方形.
是正方形.
∵![]() 45,
45,
∴△ABC是等腰直角三角形,
∴AB=BC=DE,
∵四边形ADBE是菱形,
∴四边形![]() 是正方形.
是正方形.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目