题目内容
已知AB是⊙O的直径，C是⊙O上一点，作CD⊥AB，垂足为D，延长CD到E，使DE=CD，则E点和⊙O的位置关系是（ ）
分析：首先根据已知得出△ODC≌△ODE（SAS），即可得出EO=CO，进而得出答案．
解答：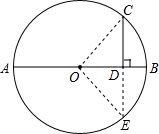
解：如图所示：连接OC，OE，
在△ODC和△ODE中
，
∴△ODC≌△ODE（SAS），
∴EO=CO，
∴点E在⊙O上．
故选：B．
解：如图所示：连接OC，OE，在△ODC和△ODE中
|
∴△ODC≌△ODE（SAS），
∴EO=CO，
∴点E在⊙O上．
故选：B．
点评：此题主要考查了点与圆的位置关系，根据已知得出CO=EO是解题关键．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
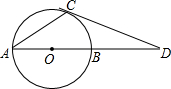如图，已知AB是⊙O的直径，∠CAB=30°，过点C的⊙O的切线交AB延长线于D，若OD=
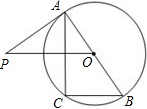如图，已知AB是⊙O的直径，过点O作弦BC的平行线，交过点A的切线AP于点P，连接AC．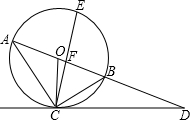
如图，已知AB是⊙O的直径，AD切⊙O于点A，