题目内容
已知AB是⊙O的直径，弧AC的度数是30°．如果⊙O的直径为4，那么AC2等于（ ）
分析：如图，连接OC．过点C作CD⊥OA于点D．根据圆心角、弧、弦间的关系知∠COD=30°．在直角△COD中，利用勾股定理、30度角所对的直角边是斜边的一半求得线段OD的长度，易求线段AD的长度．所以在直角△ACB中，利用射影定理来求AC2的值．
解答：
解：如图，连接OC．过点C作CD⊥OA于点D．
∵⊙O的直径为4，
∴AB=4，
∴OA=OC=2．
∵弧AC的度数是30°，
∴∠COD=30°，
∴CD=1，
∴OD=
=
，
则AD=2-
，
∵AB是直径，
∴∠ACB=90°．
∴AC2=AD•AB=（2-
）×4=8-4
．
故选C．
解：如图，连接OC．过点C作CD⊥OA于点D．∵⊙O的直径为4，
∴AB=4，
∴OA=OC=2．
∵弧AC的度数是30°，
∴∠COD=30°，
∴CD=1，
∴OD=
| OC2-CD2 |
| 3 |
则AD=2-
| 3 |
∵AB是直径，
∴∠ACB=90°．
∴AC2=AD•AB=（2-
| 3 |
| 3 |
故选C．
点评：本题考查了圆心角、弧、弦间的关系，勾股定理以及含30度角的直角三角形．注意，射影定理是在直角三角形中应用．
练习册系列答案
名校课堂系列答案
相关题目
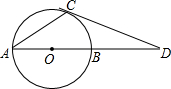如图，已知AB是⊙O的直径，∠CAB=30°，过点C的⊙O的切线交AB延长线于D，若OD=
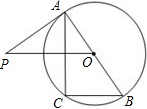如图，已知AB是⊙O的直径，过点O作弦BC的平行线，交过点A的切线AP于点P，连接AC．
如图，已知AB是⊙O的直径，AD切⊙O于点A，