题目内容
【题目】如图,抛物线y=ax2+bx﹣4与x轴交于A(4,0)、B(﹣2,0)两点,与y轴交于点C,点P是线段AB上一动点(端点除外),过点P作PD∥AC,交BC于点D,连接CP.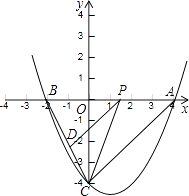
(1)求该抛物线的解析式;
(2)当动点P运动到何处时,BP2=BDBC;
(3)当△PCD的面积最大时,求点P的坐标.
【答案】
(1)解:由题意,得 ![]() ,
,
解得  ,
,
∴抛物线的解析式为y= ![]() ﹣x﹣4
﹣x﹣4
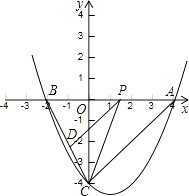
(2)解:设点P运动到点(x,0)时,有BP2=BDBC,
令x=0时,则y=﹣4,
∴点C的坐标为(0,﹣4).
∵PD∥AC,
∴△BPD∽△BAC,
∴ ![]() .
.
∵BC= ![]() =
= ![]() =2
=2 ![]() ,
,
AB=6,BP=x﹣(﹣2)=x+2.
∴BD= ![]() =
= ![]() =
= ![]() .
.
∵BP2=BDBC,
∴(x+2)2= ![]() ×2
×2 ![]() ,
,
解得x1= ![]() ,x2=﹣2(﹣2不合题意,舍去),
,x2=﹣2(﹣2不合题意,舍去),
∴点P的坐标是( ![]() ,0),即当点P运动到(
,0),即当点P运动到( ![]() ,0)时,BP2=BDBC
,0)时,BP2=BDBC
(3)解:∵△BPD∽△BAC,
∴ ![]() ,
,
∴ ![]() ×
× ![]()
S△PDC=S△PBC﹣S△PBD= ![]() ×(x+2)×4﹣
×(x+2)×4﹣ ![]()
∵ ![]() ,
,
∴当x=1时,S△PDC有最大值为3.
即点P的坐标为(1,0)时,△PDC的面积最大.
【解析】(1)利用待定系数法把AB坐标代入解析式即可;(2)先由PD∥AC可得△BPD∽△BAC,得出比例式,用x的式子表示BD,代入到 BP2=BDBC
求出x;(3)用作差法表示△PCD的面积,即S△PDC=S△PBC﹣S△PBD,构建出二次函数,用配方法求出最值.

【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:
X | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
下列结论:
⑴ac<0;
⑵当x>1时,y的值随x值的增大而减小.
⑶3是方程ax2+(b﹣1)x+c=0的一个根;
⑷当﹣1<x<3时,ax2+(b﹣1)x+c>0.
其中正确的个数为( )
A.4个
B.3个
C.2个
D.1个



