题目内容
【题目】[数学实验探索活动]
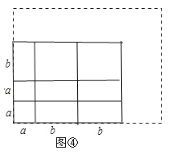
实验材料现有若干块如图①所示的正方形和长方形硬纸片.

实验目的:
用若干块这样的正方形和长方形硬纸片拼成一个新的长方形,通过不同的方法计算面积,得到相应的等式,从而探求出多项式乘法或分解因式的新途径.
例如,选取正方形、长方形硬纸片共 6 块,拼出一个如图②的长方形,计算它的面积, 写出相应的等式有 a2+3ab+2b2=(a+2b)(a+b)或 (a+2b)(a+b) =a2+3ab+2b2.
问题探索:
(1) 小明想用拼图的方法解释多项式乘法(2a+b)(a+b) =2a2+3ab+b2 ,那么需要两种正方形纸片 张,长方形纸片 张;
(2)选取正方形、长方形硬纸片共 8 块,可以拼出一个如图③的长方形,计算图③的面积,并写出相应的等式;
(3)试借助拼图的方法,把二次三项式 2a2+5ab+2b2 分解因式,并把所拼的图形画在虚线方框内.
【答案】(1)3,3;(2)a2+4ab+3b2=(a+3b)(a+b);(3)2b2+5ab+2a2=(2b+a)(b+2a).画图见解析.
【解析】
(1)根据多项式(2a+b)(a+b) =2a2+3ab+b2可发现矩形有两个小正方形,一个大正方形和三个小长方形.
(2)正方形、长方形硬纸片一共八块,面积等于长为a+3b,宽为a+b的矩形面积.所以a2+4ab+3b2=(a+3b)(a+b)
(3)正方形、长方形硬纸片共9块,画出图形,面积等于长为a+2b,宽为2a+b的矩形面积,则2a2+5ab+2b2=(2a+b)(a+2b)
(1)∵(2a+b)(a+b) =2a2+3ab+b2;
∴拼图需要两个小正方形,一个大正方形和三个小长方形
∴需要3个正方形纸片,3个长方形纸片.
(2)∵大长方形长为a+3b,宽为a+b
∴面积S=(a+3b)(a+b)
又∵大长方形由三个大正方形,一个小正方形和四个小长方形组成
∴面积S= a2+4ab+3b2
∴a2+4ab+3b2=(a+3b)(a+b)
(3)∵由2b2+5ab+2a2可知
大长方形由两个小正方形和两个大正方形以及五个长方形组成,如图
∴2b2+5ab+2a2=(2b+a)(b+2a).

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案