题目内容
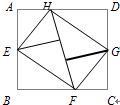18、如图，将矩形纸ABCD的四个角向内折起，恰好拼成一个无缝隙无重叠的四边形EFGH，若EH=3厘米，EF=4厘米，则边AD的长是（ ）分析：先求出△EFH是直角三角形，再根据勾股定理求出FH=5，再利用全等三角形的性质解答即可．
解答：
解：设斜线上两个点分别为P、Q则P点是B点对折过去的，
∴∠EPH为直角，△AEH≌△PEH，
∴∠HEA=∠PEH，
同理∠PEF=∠BEF，
这四个角互补，∴∠PEH+∠PEF=90°，
∴△HEF是直角三角形，∵EH=3cm，EF=4cm，
∴FH=5cm，
FH=HP+FP，
HP=AH，FP=BF，BF=HD，
∴FH=AD=5cm，
∴AD=5cm．
故选D．
解：设斜线上两个点分别为P、Q则P点是B点对折过去的，∴∠EPH为直角，△AEH≌△PEH，
∴∠HEA=∠PEH，
同理∠PEF=∠BEF，
这四个角互补，∴∠PEH+∠PEF=90°，
∴△HEF是直角三角形，∵EH=3cm，EF=4cm，
∴FH=5cm，
FH=HP+FP，
HP=AH，FP=BF，BF=HD，
∴FH=AD=5cm，
∴AD=5cm．
故选D．
点评：解答此题的关键是作出辅助线，构造出全等三角形，再根据直角三角形及全等三角形的性质解答．
练习册系列答案
期末好成绩系列答案
99加1领先期末特训卷系列答案
百强名校期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
金状元绩优好卷系列答案
相关题目
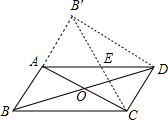到△AB′C．
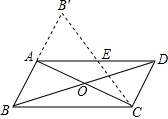180°，得到△AB′C．
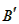为顶点的四边形是矩形；