题目内容

28、操作与探究：
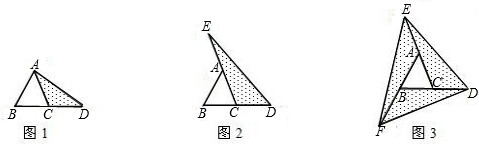
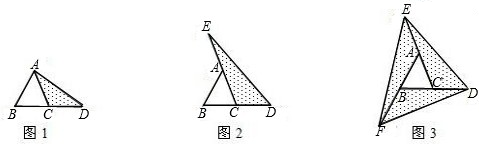
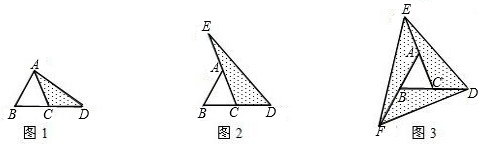
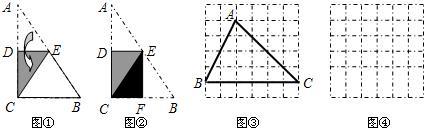
（1）图①是一块直角三角形纸片．将该三角形纸片按如图方法折叠，是点A与点C重合，DE为折痕．试证明△CBE等腰三角形；
（2）再将图①中的△CBE沿对称轴EF折叠（如图②）．通过折叠，原三角形恰好折成两个重合的矩形，其中一个是内接矩形，另一个是拼合（指无缝无重叠）所成的矩形，我们称这样的两个矩形为“组合矩形”．你能将图③中的△ABC折叠成一个组合矩形吗？如果能折成，请在图③中画出折痕；
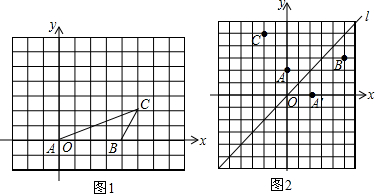
（3）请你在图④的方格纸中画出一个斜三角形，同时满足下列条件：①折成的组合矩形为正方形；②顶点都在格点（各小正方形的顶点）上；
（4）有一些特殊的四边形，如菱形，通过折叠也能折成组合矩形（其中的内接矩形的四个顶点分别在原四边形的四条边上）．请你进一步探究，一个非特殊的四边形（指除平行四边形、梯形外的四边形）满足何条件时，一定能折成组合矩形？

分析：

（1）根据折叠的性质，那么CE就与BE相等，因此三角形CBE就是个等腰三角形．
（2）可选两边的中点进行折叠，如：选AB，AC的中点D，E，沿折痕DE将A折叠刀BC上，然后将B，C两点与A点重合即可得出矩形．
（3）我们先看三角形内接正方形时各边的关系，如图：DEGH是个正方形，那么DE=HG=DH，如果我们过A引BC的垂线，交DE于N交BC于M，那么三角形BHD≌三角形DNA，三角形ANE≌三角形EGC．AN=DH=MN，BH+GC=DN+NE=DE，AN+MN=BH+GC+HG．因此AM=BC，由此可看出只要符合三角形的一边和这个边上的高相等即可通过折叠得出正方形．
（4）由于四边形的对角线都和折痕平行，那么也就是与矩形的边平行，所以四边形要想能折出一个组合矩形，那么它的对角线就应该互相垂直．

解答：

解：（1）∵点A与点C重合，
∴AD=DC，∠ADE=∠EDC，
∴DE是△ACB的中位线，
AE=BE，
∵AE=CE，
∴CE=BE，
∴△CBE是等腰三角形；

（2）如图1所示（共有三种折法，折痕画对均可）；

（3）如图2所示（答案不唯一，只要体现出一条边与该边上的高相等即可）；

（4）当一个四边形的两条对角线互相垂直时，可以折成一个组合矩形．

点评：本题主要考查了动手作图的能力，如果遇到想不出的图形，可根据几何知识，将图形中的某些特殊关系找出来，然后再动手实践．