题目内容
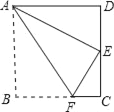
【题目】如图所示，在四边形ABCD中，AB∥CD，对角AC、BD相交于O，则图中面积相等的三角形有（ ）
A.1对B.2对C.3对D.4对
【答案】C
【解析】
根据AB∥CD可以得到AB、CD两直线间的距离是相等的，即可得到△ADC与△BDC是同底等高的三角形，△CAB与△DAB也是同底等高的三角形，可得到两对，再因为△CAB与△DAB中都含有三角形AOB，去掉之后就得到△AOD和△BOC是面积相等的一对三角形.
解：∵四边形ABCD中，AB∥CD，
∴直线AB与直线CD间的距离处处相等，
∵△ADC与△BDC的底都是DC，高都是直线AB与直线CD间的距离，
∴两个三角形同底等高，面积相等；
∵△CAB与△DAB的底都是AB，高都是直线AB与直线CD间的距离，
∴两个三角形同底等高，面积相等；
∵
,
,
其中
，
，
∴
；
综上可得一共有3对三角形面积相等，分别是：△ADC与△BDC，△CAB与△DAB，△AOD与△BOC.
故答案选C.
练习册系列答案
精英口算卡系列答案
应用题点拨系列答案
状元及第系列答案
相关题目
