题目内容
【题目】如图,在⊙O中,AB为⊙O的直径,AB=4.动点P从A点出发,以每秒π个单位的速度在⊙O上按顺时针方向运动一周.设动点P的运动时间为t秒,点C是圆周上一点,且∠AOC=40°,当t=秒时,点P与点C中心对称,且对称中心在直径AB上.
【答案】![]() 或
或 ![]() 或
或 ![]() 或
或 ![]()
【解析】解:如图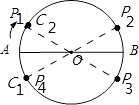 ,
,
当∠AOP1=40°时,P1与C1对称, ![]() =4π×
=4π× ![]() =
= ![]() ,t=
,t= ![]() ÷π=
÷π= ![]() ;
;
当∠AOP2=140°时,P2与C1对称, ![]() =4π×
=4π× ![]() =
= ![]() π,t=
π,t= ![]() ÷π=
÷π= ![]() ;
;
当∠AOP3=220°时,P3与C2对称, ![]() =4π×
=4π× ![]() =
= ![]() ,t=
,t= ![]() ÷π=
÷π= ![]() ;
;
当∠AOP4=320°时,P4与C1对称, ![]() =4π×
=4π× ![]() =
= ![]() π,t=
π,t= ![]() ÷π=
÷π= ![]() ;
;
所以答案是: ![]() 或
或 ![]() 或
或 ![]() 或
或 ![]() .
.
【考点精析】根据题目的已知条件,利用圆的定义和中心对称及中心对称图形的相关知识可以得到问题的答案,需要掌握平面上到定点的距离等于定长的所有点组成的图形叫做圆.定点称为圆心,定长称为半径;如果把一个图形绕着某一点旋转180度后能与另一个图形重合,那么我们就说,这两个图形成中心对称;如果把一个图形绕着某一点旋转180度后能与自身重合,那么我们就说,这个图形成中心对称图形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目