题目内容
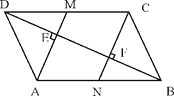
【题目】已知:如图E在△ABC的边AC上,且∠AEB=∠ABC.
⑴求证:∠ABE=∠C;
⑵若∠BAE的平分线AF交BE于F,FD∥BC交AC于D,设AB=5,AC=8,求DC的长.

【答案】(1)证明见解析(2)3
【解析】试题分析:(1)∠BAC是△ABC和△ABE的公共内角,根据三角形内角和定理即可证明∠ABE=∠C;(2)已知AF平分∠BAE,可得∠BAF=∠DAF,利用(1)所得出的结论及平行线的性质可得∠ABE=∠ADF,根据“AAS”证得△ABF≌△ADF即可得结果。
试题解析:(1)∵∠ABE=180°-∠BAC-∠AEB,∠C=180°-∠BAC-∠ABC,且∠AEB=∠ABC
∴∠ABE=∠C
(2)![]() AF平分∠BAE,
AF平分∠BAE,
∴∠BAF=∠DAF,
![]() FD∥BC,
FD∥BC,
∴∠ADF=∠C
![]() ∠ABE=∠C,
∠ABE=∠C,
∴∠ABE=∠ADF,
在△ABF与△ADF中
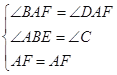
∴△ABF≌△ADF,
∴AB=AD=5
∴DC=AC-AD=3.

练习册系列答案
相关题目