题目内容
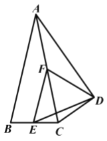
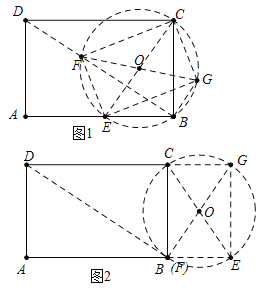
【题目】如图，矩形ABCD的边AB=3cm，AD=4cm，点E从点A出发，沿射线AD移动，以CE为直径作⊙O，点F为⊙O与射线BD的公共点，连接EF，过点E作EG⊥EF，交⊙O于点G，当⊙O与射线BD相切时，点E停止移动，则在运动过程中点G移动路程的长为（ ）
A. 4cm B. 
cm C. 
cm D. 
cm
【答案】B
【解析】解：如图1中，连接CF、CG、FG．易知四边形EFCG是矩形，∴EF=CG，∴
=
，∴∠CBG=∠ABD，∴点G的在射线BG上，∠CBG是定值，∠DBG=90°．
如图2中，当⊙O与BD相切时，F与B重合，由△BCG∽△BAD，可得
=
，∴
=
，∴BG=
cm，∴点G的运动路径的长为
cm．故选B．
练习册系列答案
名师金手指领衔课时系列答案
相关题目
