题目内容
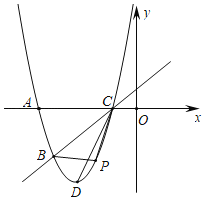
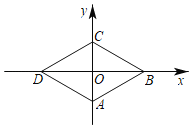
【题目】如图,已知菱形ABCD的顶点A(0,﹣1),∠DAC=60°.若点P从点A出发,沿A→B→C→D→A…的方向,在菱形的边上以每秒0.5个单位长度的速度移动,则第2020秒时,点P的坐标为( )
A.(2,0)B.(![]() ,0)C.(﹣
,0)C.(﹣![]() ,0)D.(0,1 )
,0)D.(0,1 )
【答案】B
【解析】
由菱形的性质得出AB=BC=CD=DA,OD=OB,AC⊥BD,易求OA=1,在Rt△AOD中,∠ADO=30°,得出OD=![]() OA=
OA=![]() ,AD=2OA=2,则OB=
,AD=2OA=2,则OB=![]() ,B(
,B(![]() ,0),由点P的运动速度为0.5单位长度/秒,则从点A到点B所需时间4秒,沿A→B→C→D→A所需的时间16秒,由
,0),由点P的运动速度为0.5单位长度/秒,则从点A到点B所需时间4秒,沿A→B→C→D→A所需的时间16秒,由![]() =126…4,得出移动到第2020秒和第4秒的位置相同,当P运动到第4秒时点P在点B处,即点P的坐标为(
=126…4,得出移动到第2020秒和第4秒的位置相同,当P运动到第4秒时点P在点B处,即点P的坐标为(![]() ,0),即可得出答案.
,0),即可得出答案.
解:∵四边形ABCD是菱形,
∴AB=BC=CD=DA,OD=OB,AC⊥BD,
∵A(0,﹣1),
∴OA=1,
在Rt△AOD中,
∵∠AOD=90°,∠DAC=60°,
∴∠ADO=30°,
∴OD=![]() OA=
OA=![]() ,AD=2OA=2,
,AD=2OA=2,
∴OB=![]() ,
,
∴B(![]() ,0),
,0),
∵点P的运动速度为0.5单位长度/秒,
∴从点A到点B所需时间=![]() =4(秒),
=4(秒),
∴沿A→B→C→D→A所需的时间=4×4=16(秒),
∵![]() =126…4,
=126…4,
∴移动到第2020秒和第4秒的位置相同,当P运动到第4秒时点P在点B处,即点P的坐标为(![]() ,0),
,0),
故选:B.

 小学教材全测系列答案
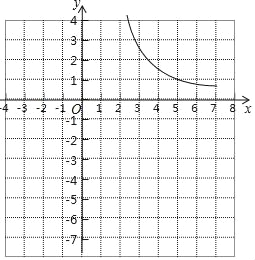
小学教材全测系列答案【题目】小邱同学根据学习函数的经验,研究函数y=![]() 的图象与性质.通过分析,该函数y与自变量x的几组对应值如下表,并画出了部分函数图象如图所示.
的图象与性质.通过分析,该函数y与自变量x的几组对应值如下表,并画出了部分函数图象如图所示.
x | 1 |
|
|
| 3 | 4 | 5 | 6 | … |
y | ﹣1 | ﹣2 | ﹣3.4 | ﹣7.5 | 2.4 | 1.4 | 1 | 0.8 | … |
(1)函数y=![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)在图中补全当1≤x<2的函数图象;
(3)观察图象,写出该函数的一条性质: ;
(4)若关于x的方程![]() =x+b有两个不相等的实数根,结合图象,可知实数b的取值范围是 .
=x+b有两个不相等的实数根,结合图象,可知实数b的取值范围是 .