Question

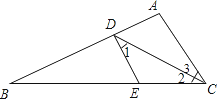
【题目】如图1，在数轴上点A，点B对应的数分别是6，﹣6，∠DCE＝90°（点C与点O重合，点D在数轴的正半轴上）

（1）如图1，若CF平分∠ACE，则∠AOF＝　 　度；点A与点B的距离=　

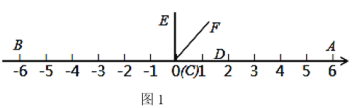
（2）如图2，将∠DCE沿数轴的正半轴向右平移t（0＜t＜3）个单位后，再绕点顶点C逆时针旋转30t度，作CF平分∠ACE，此时记∠DCF＝α．

①当t＝1时，α＝　 　；点B与点C的距离=　

②猜想∠BCE和α的数量关系，并说明理由；

（3）如图3，开始∠D1C1E1与∠DCE重合，将∠DCE沿数轴的正半轴向右平移t（0t3）个单位，再绕点顶点C逆时针旋转30t度，作CF平分∠ACE，此时记∠DCF＝α，与此同时，将∠D1C1E1沿数轴的负半轴向左平移t（0t3）个单位，再绕点顶点C1顺时针旋转30t度，作C1F1平分∠AC1E1，记∠D1C1F1＝β，若α与β满足|α﹣β|＝20°，求t的值．

Answer 1

【答案】（1）45°；12；（2）①30°；8；②，理由见解析；（3）

【解析】

（1）根据角平分线的定义计算∠AOF，根据数轴概念计算距离；
（2）①根据∠FCD＝∠ACF∠ACD，求出∠ACF，∠ACD即可；根据数轴概念即可计算距离；
②猜想：∠BCE＝2α．根据∠BCE＝∠AOB∠ECD∠ACD计算即可；
（3）求出α，β（用t表示），构建方程即可解决问题；

（1）∵∠DCE＝90°，CF平分∠ACE，

∴∠AOF＝45°，

∴答案为：45°；

点A与点B的距离为12，

∴答案为：12；

（2）①当t＝1时，

∠FCD＝∠ACF∠ACD=75°-45°=30°，

∴答案为：30°；

点B与点C的距离8，

∴答案为：8；

②猜想：∠BCE＝．

理由如下：∵∠DCE＝90°，∠DCF＝，

∴∠ECF＝90°-，

∵CF平分∠ACE，

∴∠ACF＝∠ECF＝90°-．

∵点A，O，B共线

∴AOB＝180°，

∴∠BCE＝∠AOB-∠ECD-∠ACD＝180°-90°-(90°-)＝；

（3）由题意：＝∠FCA-∠DCA＝(90°+30t)-30t＝45°-15t

＝∠AC1D1+∠AC1F1＝30t+(90°﹣30t)＝45°+15

∵||＝20°，

∴|30t|＝20°，

解得t＝．

故答案为.