题目内容
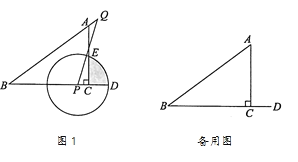
【题目】如图，海中一渔船在A处于小岛C相距70海里，若该渔船由西向东航行30海里到达B处，此时测得小岛C位于B的北偏东30°方向上，则该渔船此时与小岛C之间的距离是__海里．
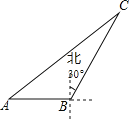
【答案】50
【解析】
过点C作CD⊥AB于点D，由题意得∠BCD＝30°，设BC＝x，解直角三角形即可得到BD＝BCsin30°＝
x、CD＝BCcos30°＝
x、AD＝30＋x，根据“AD2＋CD2＝AC2”列方程求解可得．
过点C作CD⊥AB于点D，
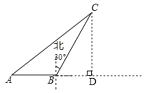
由题意得∠BCD＝30°，设BC＝x，
在Rt△BCD中，BD＝BCsin30°＝x，CD＝BCcos30°＝x；
∴AD＝30＋x，
∵AD2＋CD2＝AC2，
∴（30＋x）2＋（x）2＝702，
解得：x＝50（负值舍去），
即渔船此时与C岛之间的距离为50海里．
故答案为：50．
练习册系列答案
相关题目
