题目内容
直角三角形两锐角的平分线所夹的钝角等于( )
| A.100° | B.120° | C.135° | D.150° |
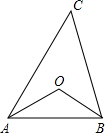
做直角三角形ABC,作AE为∠BAC的角平分线,交BC于E.
作CD为∠ACB的角平分线,交AB于D.AE与CD交于点O.
∵△ABC是直角三角形,
∴∠BAC+∠ACB=90°,
又∵AE,CD为∠BAC,∠ACB的角平分线,
∴∠CAE+∠ACD=45°,
∴∠COA=180°-(∠CAE+∠ACD)=135°,
∴∠COA=135°.
故选C.
作CD为∠ACB的角平分线,交AB于D.AE与CD交于点O.
∵△ABC是直角三角形,
∴∠BAC+∠ACB=90°,
又∵AE,CD为∠BAC,∠ACB的角平分线,
∴∠CAE+∠ACD=45°,
∴∠COA=180°-(∠CAE+∠ACD)=135°,
∴∠COA=135°.
故选C.

练习册系列答案
相关题目