题目内容
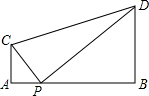如图，AC⊥AB，BD⊥AB，AB=10，AC=2；用以个三角尺进行如下操作：将直角顶点P在线段AB上滑动，一直角边始终经过点C，另一直角边与BE相交于点D，若BD=8，则AP的长为（ ）分析：首先证明∠DPB=∠C，再由∠A=∠B=90°可判定两个直角三角形相似，根据对应线段成比例可得2：AP=（10-AP）：8，解即可解答．
解答：解：∵AC⊥AB，BE⊥AB，
∴∠A=∠B=90°，
∴∠APC+∠ACP=90°
∵∠CPD=90°，
∴∠APC+∠DPB=90°，
∴∠DPB=∠C，
∴△CAP∽△PBD，
∴2：AP=（10-AP）：8，
解得AP=2或8．
∴∠A=∠B=90°，
∴∠APC+∠ACP=90°
∵∠CPD=90°，
∴∠APC+∠DPB=90°，
∴∠DPB=∠C，
∴△CAP∽△PBD，
∴2：AP=（10-AP）：8，
解得AP=2或8．
点评：本题主要考查了相似三角形的判定与性质，关键是掌握判定两个三角形相似的方法以及相似三角形的性质．
练习册系列答案
相关题目
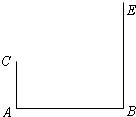21、如图，AC⊥AB，BE⊥AB，AB=10，AC=2．用一块三角尺进行如下操作：将直角顶点P在线段AB上滑动，一直角边始终经过点C，另一直角边与BE相交于点D，若BD=8，则AP的长为
4、如图，AC=AB，AD平分∠CAB，E在AD上，则图中能全等的三角形有（ ）对．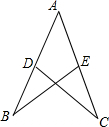
如图，AC=AB，BD=CE，若∠B=25°，则∠C=
如图，AC⊥AB，AD⊥AE，且AB=AC，AD=AE，探究BD与CE的关系．