题目内容
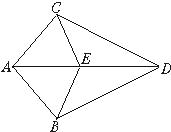4、如图，AC=AB，AD平分∠CAB，E在AD上，则图中能全等的三角形有（ ）对．分析：根据全等三角形的判定定理SAS得出△CAE≌△BAE和△CAD≌△BAD，通过△CAD≌△BAD，得出△CAD≌△BAD．
解答：解：∵AD平分∠CAB，
∴∠CAE=∠EAB，
又因为AC=AB，AE=AE，
∴△CAE≌△BAE；
∵AD平分∠CAB，
∴∠CAE=∠EAB，
又因为AC=AB，AD=AD，
∴△CAD≌△BAD；
∵△CED≌△BED；
∴CD=BD，∠CDA=∠BDA，
∴△CAD≌△BAD．
故选C．
∴∠CAE=∠EAB，
又因为AC=AB，AE=AE，
∴△CAE≌△BAE；
∵AD平分∠CAB，
∴∠CAE=∠EAB，
又因为AC=AB，AD=AD，
∴△CAD≌△BAD；
∵△CED≌△BED；
∴CD=BD，∠CDA=∠BDA，
∴△CAD≌△BAD．
故选C．
点评：主要考查了三角形全等的判定定理：有两边及其夹角对应相等的两个三角形全等．运用定理来判定两三角形全等．
练习册系列答案
相关题目
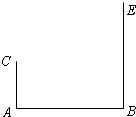21、如图，AC⊥AB，BE⊥AB，AB=10，AC=2．用一块三角尺进行如下操作：将直角顶点P在线段AB上滑动，一直角边始终经过点C，另一直角边与BE相交于点D，若BD=8，则AP的长为
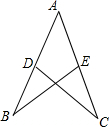如图，AC=AB，BD=CE，若∠B=25°，则∠C=
如图，AC⊥AB，AD⊥AE，且AB=AC，AD=AE，探究BD与CE的关系．