ЬтФПФкШн
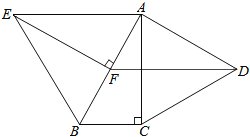
ЁОЬтФПЁПШчЭМЃЌвбжЊЁїABCКЭЁїDEFЪЧСНИіБпГЄЖМЮЊ1 cmЕФЕШБпШ§НЧаЮЃЌЧвBЃЌDЃЌCЃЌEЖМдкЭЌвЛжБЯпЩЯЃЌСЌНгADМАCF.
(1)ЧѓжЄЃКЫФБпаЮADFCЪЧЦНааЫФБпаЮЃЛ
(2)ШєBDЃН0.3 cmЃЌЁїABCбизХBEЕФЗНЯђвдУПУы1 cmЕФЫйЖШдЫЖЏЃЌЩшЁїABCЕФдЫЖЏЪБМфЮЊtУыЃЎ
ЂйЕБtЮЊКЮжЕЪБЃЌ ![]() ADFCЪЧСтаЮЃПЧыЫЕУїФуЕФРэгЩЃЛ
ADFCЪЧСтаЮЃПЧыЫЕУїФуЕФРэгЩЃЛ
Ђк![]() ADFCгаПЩФмЪЧОиаЮТ№ЃПШєПЩФмЃЌЧѓГіtЕФжЕМАДЫОиаЮЕФУцЛ§ЃЛШєВЛПЩФмЃЌЧыЫЕУїРэгЩЃЎ
ADFCгаПЩФмЪЧОиаЮТ№ЃПШєПЩФмЃЌЧѓГіtЕФжЕМАДЫОиаЮЕФУцЛ§ЃЛШєВЛПЩФмЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПМћНтЮі
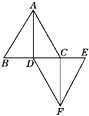
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉИљОнвбжЊЬѕМўПЩжЊACЁЮDFЃЌМДПЩЕУГіЫФБпаЮADFCЪЧЦНааЫФБпаЮЃЌ
ЃЈ2ЃЉИљОнЁїABCбизХBEЕФЗНЯђвдУПУы1cmЕФЫйЖШдЫЖЏЃЌЫљвдЕБt=![]() УыЪБЃЌBгыDжиКЯЃЌетЪБЫФБпаЮЮЊСтаЮЃЌ
УыЪБЃЌBгыDжиКЯЃЌетЪБЫФБпаЮЮЊСтаЮЃЌ
ЃЈ3ЃЉШєЦНааЫФБпаЮADFCЪЧОиаЮЃЌдђЁЯADF=90ЁуЃЌEгыBжиКЯЃЌЕУГіt=1.3УыЃЌПЩЧѓГіДЫЪБОиаЮЕФУцЛ§ЃЎ
ЪдЬтНтЮіЃК
ЃЈ1ЃЉЁпЁїABCКЭЁїDEFЪЧСНИіБпГЄЖМЮЊlcmЕФЕШБпШ§НЧаЮЃЌ
ЁрAC=DF=1cmЃЌЁЯACB=ЁЯFDE=60ЁуЃЌ
ЁрACЁЮDFЃЌ
ЁрЫФБпаЮADFCЪЧЦНааЫФБпаЮЃЛ
ЃЈ2ЃЉЂйЕБt=0.3УыЪБЃЌЦНааЫФБпаЮADFCЪЧСтаЮЃЌРэгЩШчЯТЃК
ЁпЁїABCбизХBEЕФЗНЯђвдУПУы1cmЕФЫйЖШдЫЖЏЃЌ
ЁрЕБt=![]() УыЪБЃЌBгыEжиКЯЃЌШчЭМЫљЪОЃЌ
УыЪБЃЌBгыEжиКЯЃЌШчЭМЫљЪОЃЌ

дђAD=AE=BC=DE=DF=EFЃЌ
ЁрЦНааЫФБпаЮADFCЪЧСтаЮЃЌ
ЂкШєЦНааЫФБпаЮADFCЪЧОиаЮ,дђЁЯADF=90ЁуЃЌ
ЁрЁЯADC=9060=30Ёу
ЭЌРэЁЯDAB=30Ёу=ЁЯADCЃЌ
ЁрBA=BDЃЌ
ЭЌРэEC=EFЃЌ
ЁрEгыBжиКЯЃЌ
Ёрt=(1+0.3)ЁТ1=1.3УыЃЌ
ДЫЪБЃЌШчЭМЃЌ
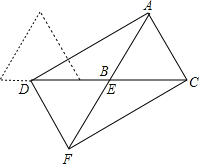
дкRtЁїADFжаЃЌ
ЁЯADF=90ЁуЃЌDF=1cmЃЌAF=2cmЃЌ
ЁрAD=![]() cmЃЌ
cmЃЌ
ЁрОиаЮADFCЕФУцЛ§=ADЁСDF=![]() cm2.
cm2.