题目内容
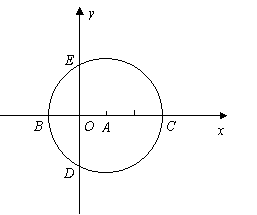
如图,在直角坐标系中,以点![]() 为圆心,以
为圆心,以![]() 为半径的⊙A与
为半径的⊙A与![]() 轴相交于点
轴相交于点![]() ,与
,与![]() 轴相交于点
轴相交于点![]() .
.
(1)若抛物线![]() 经过
经过![]() 两点,求抛物线的解析式,并判断点
两点,求抛物线的解析式,并判断点![]() 是否在该抛物线上;
是否在该抛物线上;
(2)在(1)中的抛物线的对称轴上求一点![]() ,使得
,使得![]() 的周长最小;
的周长最小;
(3![]() )设
)设![]() 为(1)中的抛物线的对称轴上的一点,在抛物线上是否存在这样的点
为(1)中的抛物线的对称轴上的一点,在抛物线上是否存在这样的点![]() ,使得以B、C、Q、M为顶点的四边形是平行四边形?∠若存在,求出点
,使得以B、C、Q、M为顶点的四边形是平行四边形?∠若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
解:(1)
解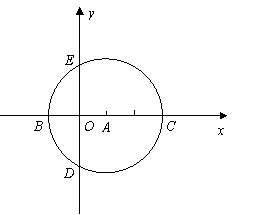 :(1)∵
:(1)∵![]() ,⊙A的半径为
,⊙A的半径为![]()
∴OA=![]() ,AD=
,AD=![]()
![]() ,
,![]()
在![]() 中,
中,![]() ,
,![]()
∴OD=3,![]()
![]() 的坐标为
的坐标为![]()
∵抛物线![]() 过
过![]() 两点,
两点,
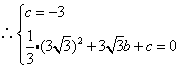
∴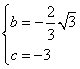
![]() 所求抛物线的解析式为:
所求抛物线的解析式为:![]()
当![]() 时,
时,![]()
![]() 点
点![]() 在抛物线上
在抛物线上
(2)![]()
![]()
![]() 抛物线
抛物线![]() 的对称轴方程为
的对称轴方程为![]()
在抛物线的对称轴上存在点![]() ,使
,使![]() 的周长最小.
的周长最小.
![]() 的长为定值
的长为定值 ![]() 要使
要使![]() 周长最小只需
周长最小只需![]() 最小.
最小.
连结![]() ,则
,则![]() 与对称轴的交点即为使
与对称轴的交点即为使![]() 周长最小的点.
周长最小的点.
∵直线![]() 的解析式为
的解析式为![]()
当x=![]() 时,y=-2,
时,y=-2,
∴所求点![]() 的坐标为
的坐标为![]()
(3)在抛物线上存在点![]() ,使得以B、C、Q
,使得以B、C、Q![]() 、M为顶点的四边形是平行四边形.
、M为顶点的四边形是平行四边形.
∵BC=4![]()
① 当BC为平行四边形的边,且点M在抛物线对称轴的左侧时,
所求M点的坐标是![]() (-3
(-3![]() ,12)
,12)
② 当BC为平行四边形的边,且点M在抛物线对称轴的右侧时,
所求M点的坐标是![]() (5
(5![]() ,12)
,12)
③当BC为平行四边形的对角线时,所求M点的坐标是![]() (
(![]() ,4)-----9分
,4)-----9分
综上所述:在抛物线上存在点![]() ,使得以B、C、Q、M为顶点的四边形是平行四边形,且所求M的坐标为
,使得以B、C、Q、M为顶点的四边形是平行四边形,且所求M的坐标为![]() (-3
(-3![]() ,12)、
,12)、![]() (5
(5![]() ,12)、
,12)、
![]() (
(![]() ,4).
,4).

练习册系列答案
相关题目

 如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.

 ,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件:
,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件: