题目内容
【题目】如图,在四边形ABCD中,AB=3,BC=4,CD=12,AD=13,∠B=90°,则四边形ABCD的面积是( ) 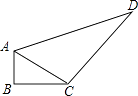
A.36
B.40
C.![]()
D.38
【答案】A
【解析】解:在Rt△ABC中,∠B=90°,AB=3,BC=4,由勾股定理得:AC= ![]() =5,
=5,
∵AD=13,DC=12,
∴AC2+CD2=AD2,
∴∠ACD=90°,
∴四边形ABCD的面积S=S△ABC+S△ACD= ![]() +
+ ![]()
= ![]() ×
× ![]()
=36.
故选A.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对勾股定理的逆定理的理解,了解如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形.

【题目】某校为了备战2018体育中考,因此在八年级抽取了50名女学生进行“一分钟仰卧起坐”测试,测试的情况绘制成表格如下:
个数 | 16 | 22 | 25 | 28 | 29 | 30 | 35 | 37 | 40 | 42 | 45 | 46 |
人数 | 2 | 1 | 7 | 18 | 1 | 9 | 5 | 2 | 1 | 1 | 1 | 2 |
(1)通过计算算得出这50名女学生进行“一分钟仰卧起坐”的平均数是 , 请写出这50名女学生进行“一分钟仰卧起坐”的众数和中位数,它们分别是、 .
(2)学校根据测试数据规定八年级女学生“一分钟仰卧起坐”的合格标准为28次,已知该校五年级有女生250名,试估计该校五年级女生“一分钟仰卧起坐”的合格人数是多少?
【题目】商场某柜台销售每台进价分别为160元、120元的A、B两种型号的电风扇,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 4台 | 1200元 |
第二周 | 5台 | 6台 | 1900元 |
(进价、售价均保持不变,利润=销售收入﹣进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若商场准备用不多于7500元的金额再采购这两种型号的电风扇共50台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,商场销售完这50台电风扇能否实现利润超过1850元的目标?若能,请给出相应的采购方案;若不能,请说明理由.