题目内容
【题目】在数学活动课上，王老师出示一道数学题目：“在平面直角坐标系
中，当
为何值时，抛物线
与直线段
有唯一公共点或有两个公共点？”某学习小组经探究得到以下四个结论：
①当
时，有唯一公共点；
②若为整数，则仅当的值为4或5或6或7时，才有唯一公共点；
③若为整数，则当的值为1或2或3时，有两个公共点；
④当
时，有两个公共点．其中正确的结论有（ ）
A.①②④B.①②③C.①③D.①④
【答案】B
【解析】
根据抛物线表达式得出其对称轴，分别求出抛物线和直线段有不同交点数时对应的c的值，从而判断各个选项.
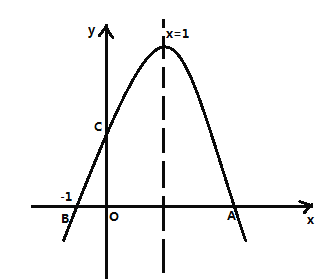
解：由抛物线表达式得：
，对称轴为直线x=2，
如图，当
时，
，联立
，
得：
，变形得：
，
解得：x1=x2=
，
∴此时抛物线和直线段只有一个交点，故①正确；
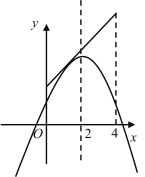
如图，当抛物线经过直线段与y轴交点时，
将x=0代入y=x+3，得y=3，
此时抛物线过（0，3），
即c=3，
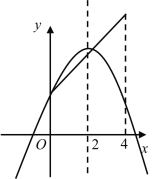
如图，当抛物线经过直线段右侧端点时，
将x=4代入y=x+3，得y=7，
此时抛物线过（4，7），代入，
得：c=7，
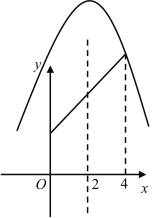
综上：当c＜
时，抛物线与直线段无公共点，
当c=时，抛物线与直线段有一个公共点，
当＜c≤3时，抛物线与直线段有两个公共点，
当3＜c≤7时，抛物线与直线段有一个公共点，
当c＞7时，抛物线与直线段无公共点，
据此可得：
若
为整数，则仅当的值为4或5或6或7时，才有唯一公共点，正确；
若为整数，则当的值为1或2或3时，有两个公共点，正确；
当
时，有两个公共点，错误.
即①②③正确，
故选B.
练习册系列答案
相关题目
