Question

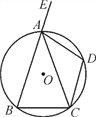
【题目】如图，在△ABC中，AB＝AC，⊙O是△ABC的外接圆，D为弧AC的中点，E是BA延长线上一点，∠DAE＝105°．

(1)求∠CAD的度数；

(2)若⊙O的半径为3，求弧BC的长.

Answer 1

【答案】(1) 35°;(2) .

【解析】

（1）由已知易得，由此可得∠ACB=2∠ACD，由∠DAE=105°，四边形ABCD是⊙O的内接四边形易得∠BCD=105°，由此可得3∠ACD=105°，从而可得∠ACD=35°；

（2）由（1）中结论易得∠ABC=∠ACB=70°，由此可得∠BAC=40°，连接OB、OC，则可得∠BOC=80°，这样由弧长计算公式即可求出的长度了.

(1)∵AB=AC，

∴，

∵D是的中点，

∴，

∴，

∴∠ACB=2∠ACD，

∵四边形ABCD内接于⊙O，

∴∠BCD=∠EAD=105°

∴∠ACB+∠ACD=105°，即3∠ACD=105°，

∴∠CAD=∠ACD=35°

(2)∵AB=AC，

∴∠ABC=∠ACB=70°，

∴∠BAC=40°，

连结OB，OC，则∠BOC=2∠BAC =80°，

∴的长.