题目内容
已知关于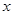 的方程
的方程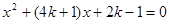 。
。
(1)求证此方程一定有两个不相等的实数根。
(2)设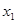 、
、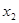 是方程的两个实数根,且(
是方程的两个实数根,且(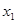 -2)(
-2)(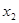 -2)=2
-2)=2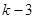 ,求
,求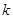 的值。
的值。
【答案】
证明:(1)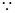 a=1,b=4k+1,c=2k-1
a=1,b=4k+1,c=2k-1
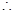
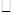 =b2-4ac
=b2-4ac
=(4k+1)2-4×1×(2k-1)
=16k2+5
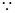 k2
k2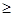 0,
0,
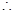 16k2+5>0, 即
16k2+5>0, 即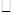 >0,
>0,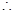 原方程一定有两个不相等的实数根。
原方程一定有两个不相等的实数根。
(2)解:依题意得
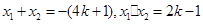
又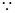 (
(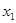 -2)(
-2)(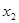 -2)=2
-2)=2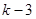 ,
,
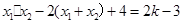
即 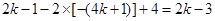
解得k=—1
【解析】(1)先表示出根的判别式即可得到结果;
(2)由根与系数的关系即可得到关于k的分程。

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
已知关于的方程
=-1有正根,则实数a的取值范围是( )
| x+a |
| x-3 |
| A、a<0且a≠-3 |
| B、a>0 |
| C、a<-3 |
| D、a<3且a≠-3 |
 的方程
的方程 .
.
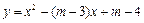 与
与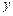 轴交于点M,若抛物线与x轴的一个交点关于直线
轴交于点M,若抛物线与x轴的一个交点关于直线 的对称点恰好是点M,求
的对称点恰好是点M,求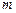 的值.
的值.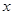 的方程
的方程
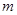 的值,并求出此时方程的根(6分)
的值,并求出此时方程的根(6分)