��Ŀ����
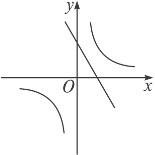
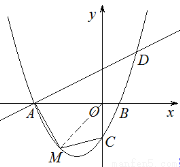
��ͼ����֪������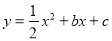 ��x�ύ��A��B���㣬�Գ���Ϊֱ��
��x�ύ��A��B���㣬�Գ���Ϊֱ��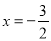 ��ֱ��AD���������ڵ�D��2��3����
��ֱ��AD���������ڵ�D��2��3����
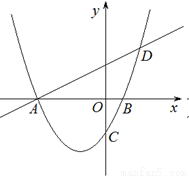
��1���������ߵĽ���ʽ��
��2����֪��MΪ�����������������ϵ�һ���㣬����M��ʲôλ��ʱ�ı���AMCO��������������ֵ��
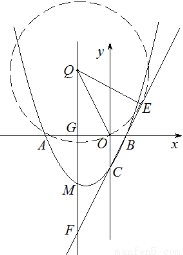
��3�����ı���AMCO������ʱ������M��ֱ��ƽ����y�ᣬ������ֱ�����Ƿ����һ����Q��ΪԲ�ģ�OQΪ�뾶����ֱ��BC���е�Բ�������ڣ����Բ��Q�����ꣻ�������ڣ���˵�����ɣ�
��1�������ߵĽ���ʽΪ .��
.��
(2) ����MΪ(��2����3)ʱ�ı���AMCO��������ֵ�����ֵΪ8��
(3) ����һ����Q��ΪԲ�ģ�OQΪ�뾶����ֱ��BC���е�Բ����Q������Ϊ����2��4����2����1��������
��������
�����������1���ɴ���ϵ�������ɵã�
��2������OM�����ı���AMCO�ɷ�Ϊ���������Σ���M������꣬��ɱ�ʾ�����������ε�����������ɵõ���������ֵ
��3�������ȼ�����������ĵ㣬Ȼ��������е��������м��㼴��
�����������1����������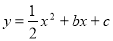 �ĶԳ�����ֱ��
�ĶԳ�����ֱ��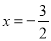 ,
,
�� �����
�����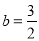 .
.
��������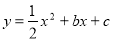 ����D(2,3),
����D(2,3),
��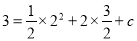 �����
�����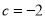 .
.
�������ߵĽ���ʽΪ .
.
��2�������ߵĽ���ʽΪ��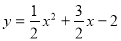 ,
,
��x��0����y����2����C��0�� -2����
��y��0����x����4��1����A(-4��0)��B��1��0����
���M����Ϊ(m��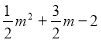 )������MO��
)������MO��
��S�ı���AMCO��S��AMO��S��CMO
��
��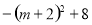
�൱m����2ʱ��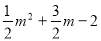 ����3
����3
�൱��MΪ(��2����3)ʱ�ı���AMCO��������ֵ�����ֵΪ8������
��3��������������ġ�Q��
��ֱ��x����2��x�ύ�ڵ�G����ֱ��BC���ڵ�F����ֱ��BC�Ľ���ʽΪy��kx��b��
��B��1��0����C��0����2������ã�
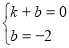 ����ã�k��2��b����2��
����ã�k��2��b����2��
��ֱ��BC����ʽΪ��y��2x��2��
��x����2����y����6����F����2����6����GF��6��
��Rt��BGF�У��ɹ��ɶ����ã�
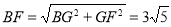 ,
,
��Q����2��n��������Rt��QGO�У��ɹ��ɶ����ã�
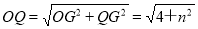 .
.
���Q��ֱ��BC�����ڵ�E����QE��OQ��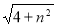 ��
��
��Rt��BGF��Rt��QEF��
�ߡ�BGF����QEF��90�㣬��BFG����QFE��
��Rt��BGF��Rt��QEF.
�� ����
���� .
.
����ã�n2��3n��4��0�����n��4��n����1��
�����һ����Q��ΪԲ�ģ�OQΪ�뾶����ֱ��BC���е�Բ����Q������Ϊ����2��4����2����1����
���㣺1������ϵ������2�����κ��������ʣ�3�����ɶ�����4�����ߵ�����

 ���������ʱ��ѵϵ�д�
���������ʱ��ѵϵ�д� �㽭�¿γ���άĿ�������ʱ��ѵϵ�д�
�㽭�¿γ���άĿ�������ʱ��ѵϵ�д� ��������ϵ�д�
��������ϵ�д� ���ɶ���ܲ��¿�ֱͨ�߿�ϵ�д�
���ɶ���ܲ��¿�ֱͨ�߿�ϵ�д�