Ő‚ńŅńŕ»›
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨“‘÷ĪŌŖAB…Ō“ĽĶ„Oő™∂ňĶ„◊ų…šŌŖOC£¨ Ļ°ŌBOC=70°„£¨Ĺę“ĽłŲ÷ĪĹ«»żĹ«įŚĶń÷ĪĹ«∂•Ķ„∑Ň‘ŕĶ„Oī¶£ģ£®◊Ę£ļ°ŌDOE=90°„£©
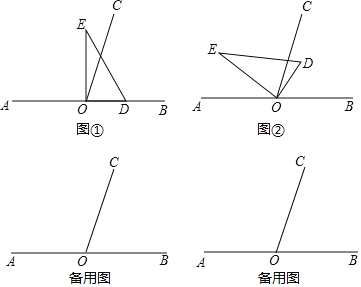
£®1£©»ÁÕľĘŔ£¨»Ű÷ĪĹ«»żĹ«įŚDOEĶń“ĽĪŖOD∑Ň‘ŕ…šŌŖOB…Ō£¨‘Ú°ŌCOE=°° °°°„£Ľ
£®2£©»ÁÕľĘŕ£¨Ĺę÷ĪĹ«»żĹ«įŚDOE»∆Ķ„O◊™∂Į£¨»ÁĻŻOD‘ŕ°ŌBOCĶńńŕ≤Ņ£¨«“°ŌBOD=50°„£¨«ů°ŌCOEĶń∂» ż£Ľ
£®3£©Ĺę÷ĪĹ«»żĹ«įŚDOE»∆Ķ„O◊™∂Į£¨»ÁĻŻOD‘ŕ°ŌBOCĶńÕ‚≤Ņ£¨«“°ŌBOD=80°„£¨«Ž‘ŕĪł”√Õľ÷–Ľ≠≥Ų»żĹ«įŚDOEĶńőĽ÷√£¨≤Ę«ů≥Ų°ŌCOEĶń∂» ż£ģ
°ĺīūįł°Ņ£®1£©20°„£Ľ£®2£©°ŌCOEĶń∂» żő™70°„£Ľ£®3£©Ľ≠ÕľľŻĹ‚őŲ£¨°ŌCOEĶń∂» żő™100°„ĽÚ60°„£ģ
°ĺĹ‚őŲ°Ņ
£®1£©»ÁÕľĘŔ£¨»Ű÷ĪĹ«»żĹ«įŚDOEĶń“ĽĪŖOD∑Ň‘ŕ…šŌŖOB…Ō£¨‘Ú°ŌCOE=20°„£Ľ
£®2£©»ÁÕľĘŕ£¨Ĺę÷ĪĹ«»żĹ«įŚDOE»∆Ķ„O◊™∂Į£¨»ÁĻŻOD‘ŕ°ŌBOCĶńńŕ≤Ņ£¨«“°ŌBOD=50°„£¨Ņ…÷™°ŌCOD=20ĹÝ∂ÝŅ…«ů°ŌCOEĶń∂» ż£Ľ
£®3£©Ĺę÷ĪĹ«»żĹ«įŚDOE»∆Ķ„O◊™∂Į£¨»ÁĻŻOD‘ŕ°ŌBOCĶńÕ‚≤Ņ£¨«“°ŌBOD=80°„£¨‘ŕĪł”√Õľ÷–Ľ≠≥Ų»żĹ«įŚDOEĶńŃĹłŲőĽ÷√£¨ľīŅ…«ů≥Ų°ŌCOEĶń∂» ż£ģ
£®1£©»ÁÕľĘŔ£¨»Ű÷ĪĹ«»żĹ«įŚDOEĶń“ĽĪŖOD∑Ň‘ŕ…šŌŖOB…Ō£¨‘Ú°ŌCOE=°ŌDOE©Ā°ŌBOC=90°„©Ā70°„=20°„£ģ
Ļ īūįłő™£ļ20°„£Ľ
£®2£©»ÁÕľĘŕ£¨Ĺę÷ĪĹ«»żĹ«įŚDOE»∆Ķ„O◊™∂Į£¨»ÁĻŻOD‘ŕ°ŌBOCĶńńŕ≤Ņ£ģ
°Ŗ°ŌBOD=50°„£¨
°ŗ°ŌCOD=°ŌBOC©Ā°ŌBOD=70°„©Ā50°„=20°„£¨
°ŗ°ŌCOE=°ŌDOE©Ā°ŌCOD=90°„©Ā20°„=70°„£¨
īū£ļ°ŌCOEĶń∂» żő™70°„£Ľ
£®3£©Ĺę÷ĪĹ«»żĹ«įŚDOE»∆Ķ„O◊™∂Į£¨»ÁĻŻOD‘ŕ°ŌBOCĶńÕ‚≤Ņ£¨«“°ŌBOD=80°„£¨∑÷ŃĹ÷÷«ťŅŲŐ÷¬Ř£ļ
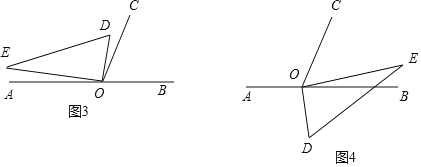
ĘŔÕľ3÷–£¨°Ŗ°ŌBOD=80°„£¨°ŌBOC=70°„£¨
°ŗ°ŌDOC=°ŌBOD©Ā°ŌBOC=10°„£¨
°ŗ°ŌCOE=°ŌCOD+°ŌDOE=10°„+90°„=100°„£ģ
ĘŕÕľ4÷–£¨°Ŗ°ŌBOE=°ŌDOE©Ā°ŌBOD=90°„©Ā80°„=10°„£¨
°ŗ°ŌCOE=°ŌBOC©Ā°ŌBOE=70°„©Ā10°„=60°„£ģ
◊Ř…Ōňý Ų£ļ°ŌCOEĶń∂» żő™100°„ĽÚ60°„£ģ
īū£ļ°ŌCOEĶń∂» żő™100°„ĽÚ60°„£ģ

°ĺŐ‚ńŅ°Ņń≥Ļ§≥ßő™ŃňĹ‚ľ◊°Ę““ŃĹłŲ≤Ņ√Ň‘ĪĻ§Ķń…ķ≤ķľľń‹«ťŅŲ£¨ī”ľ◊°Ę““ŃĹłŲ≤Ņ√ŇłųňśĽķ≥ť»°20√Ż‘ĪĻ§£¨ĹÝ––…ķ≤ķľľń‹≤‚ ‘£¨≤‚ ‘≥…ľ®£®įŔ∑÷÷∆£©»ÁŌ¬£ļ
ľ◊7886 748175768770759075798170748086698377
““9373 888172819483778380817081737882807040
£®ňĶ√ų£ļ≥…ľ®80∑÷ľį“‘…Ōő™”Ň–„£¨70-79∑÷ő™Ńľļ√£¨60-69∑÷ő™ļŌłŮ£¨60∑÷“‘Ō¬ő™≤ĽļŌłŮ£©
£®1£©«ŽŐÓÕÍ’ŻĪŪłŮ£ļ
≤Ņ√Ň | ∆Ĺĺý ż | ÷–őĽ ż | ÷ŕ ż |
ľ◊ | 78.3 | 75 | |
““ | 78 | 80.5 |
£®2£©ī”—ýĪĺ żĺ›Ņ…“‘Õ∆∂Ō≥Ų ≤Ņ√Ň‘ĪĻ§Ķń…ķ≤ķľľń‹ňģ∆ĹĹŌłŖ£¨«ŽňĶ√ųņŪ”…£ģ£®÷Ń…Ŕī”ŃĹłŲ≤ĽÕ¨ĶńĹ«∂»ňĶ√ųÕ∆∂ŌĶńļŌņŪ–‘£©£ģ