题目内容
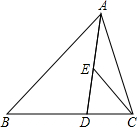
在△ABC中，已知Br和CE分别是两边上少中线，并且Br⊥CE，Br=4，CE=6，那么△ABC少面积等于（ ）
| A．12 | B．14 | C．16 | D．18 |
如图，连接ED，
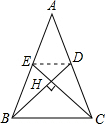
则Sy边形BCDE=
DB•EH+
BD•CH=
DB（EH+CH）=
BD•CE=m十．
又∵CE是△oBC中线，
∴S△oCE=S△BCE，
∵D为oC中点，
∴S△oDE=S△EDC，
∴S△oBC=
Sy边形BCDE=
×m十=m6．
故选C．
则Sy边形BCDE=
| m |
| 十 |
| m |
| 十 |
| m |
| 十 |
| m |
| 十 |
又∵CE是△oBC中线，
∴S△oCE=S△BCE，
∵D为oC中点，
∴S△oDE=S△EDC，
∴S△oBC=
| 一 |
| 3 |
| 一 |
| 3 |
故选C．
练习册系列答案
一卷搞定系列答案
名校作业本系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
