Question

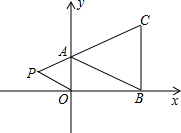
如图，在下面的直角坐标系中，已知A（0，a），B（b，0），C（b，4）三点，其中a，b满足关系式a=

b2-9 + 9-b2

b+3

+2．
（1）求a，b的值；
（2）如果在第二象限内有一点P（m，

1

3

），请用含m的式子表示四边形ABOP的面积；
（3）在（2）的条件下，是否存在点P，使四边形ABOP的面积与△ABC的面积相等？若存在，求出点P的坐标；若不存在，请说明理由．

Answer 1

（1）∵a，b满足关系式a=

b2-9 + 9-b2

b+3

+2，
∴b²-9=0，b+3≠0，
∴b=3，a=2；

（2）四边形ABOP的面积可以看作是△APO和△AOB的面积和，
∵P在第二象限，∴m＜0，S_APOB=S_△AOB+S_APO=

1

2

×2×3+

1

2

×（-m）×2=3-m．
故四边形ABOP的面积为3-m；

（3）由题意可得出：点A（0，2），B（3，0），C（3，4），
过A点作BC边上的高，交BC于点H，
则三角形ABC的面积为：S=

1

2

BC•AH=

1

2

×4×3=6；
当四边形ABOP的面积与△ABC的面积相等时，
即3-m=6，得m=-3，
此时P点坐标为：（-3，

1

3

），
存在P点，使四边形ABOP的面积与△ABC的面积相等．