题目内容
【题目】如图,在平面直角坐标系中,已知B(8,0),C(0,6),P(﹣3,3),现将一直角三角板EPF的直角顶点放在点P处,EP交y轴于N,FP交x轴于M,把△EPF绕点P旋转:
(1)如图甲,①求OM+ON的值;
②求BM﹣CN的值;
(2)如图乙,①求ON﹣OM的值;
②求BM+CN的值.
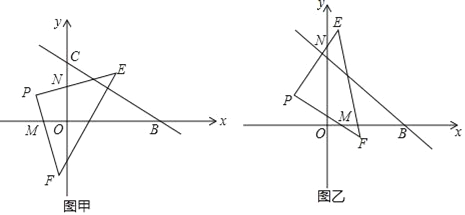
【答案】(1)6,8;(2)6,8.
【解析】试题分析:(1)如图甲中,①作PG⊥x轴于G,PH⊥y轴于H,得到矩形PGOH,根据矩形的性质和全等三角形的判定定理证明△NPH≌△MPG,得到NH=MG,根据图形的性质得到答案.②根据②BM-CN=OB+OM-(OC-ON)=OB-OC+OM+ON计算即可.
(2)如图乙中,①作PG⊥x轴于G,PH⊥y轴于H,由△NPH≌△MPG,推出NH=MG,推出ON-OM=(OH+HN)-(GM-OG)=OG+OH=6.
②根据BM+CN=(OB-OM)+(ON-OC)=OB-OC+ON-OM计算即可.
试题解析:(1)如图甲中,①作PG⊥x轴于G,PH⊥y轴于H,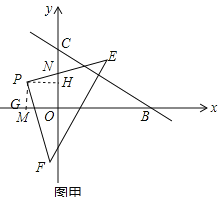
∵四边形PGOH为矩形,
∴∠HPG=90°,又∠EPF=90°,
∴∠NPH=∠MPG,
∵P(-3,3),
∴PH=PG=3,
在△NPH和△MPG中,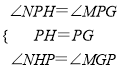 ,
,
∴△NPH≌△MPG,
∴NH=MG,
∴OM+ON=(OG-GM)+(HN+OH)=OG+OH=6.
②BM-CN=OB+OM-(OC-ON)=OB-OC+OM+ON=8-6+6=8.
(2)如图乙中,①作PG⊥x轴于G,PH⊥y轴于H,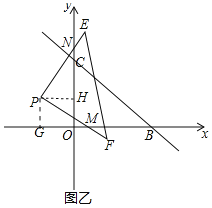
∵四边形PGOH为矩形,
∴∠HPG=90°,又∠EPF=90°,
∴∠NPH=∠MPG,
∵P(-3,3),
∴PH=PG=3,
在△NPH和△MPG中,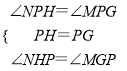 ,
,
∴△NPH≌△MPG,
∴NH=MG,
∴ON-OM=(OH+HN)-(GM-OG)=OG+OH=6.
②BM+CN=(OB-OM)+(ON-OC)=OB-OC+ON-OM=8-6+6=8.

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案【题目】七年级一班和二班各推选10名同学进行投篮比赛,按照比赛规则,每人各投了10个球,两个班选手的进球数统计如下表,请根据表中数据回答下列问题.
进球数/个 | 10 | 9 | 8 | 7 | 6 | 5 |
一班人数/人 | 1 | 1 | 1 | 4 | 0 | 3 |
二班人数/人 | 0 | 1 | 2 | 5 | 0 | 2 |
(1)分别求一班和二班选手进球数的平均数、众数、中位数.
(2)如果要从这两个班中选出一个班代表本年级参加学校的投篮比赛,争取夺得总进球数团体第一名,你认为应该选择哪个班?如果要争取个人进球数进入学校前三名,你认为应该选择哪个班?