��Ŀ����
����Ŀ����ͼ1����OΪֱ��AB��һ�㣬����O������OC��ʹ��BOC=120�㣬��һֱ�����ǰ��ֱ�Ƕ�����ڵ�O����һ��OM������OB�ϣ���һ��ON��ֱ��AB���·��� 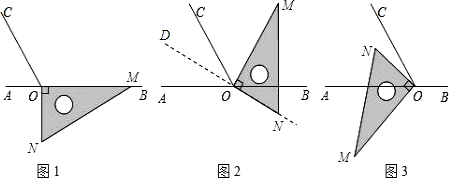
��1����ͼ1�е����ǰ��Ƶ�O��ʱ����ת��ͼ2��ʹһ��OM�ڡ�BOC���ڲ�����ǡ��ƽ�֡�BOC����ON�ķ����ӳ���ΪOD�����COD=�㣬��AOD=�㣮
��2����ͼ1�е����ǰ��Ƶ�O˳ʱ����ת��ͼ3��ʹON�ڡ�AOC���ڲ������AOM����NOC�Ķ�����
���𰸡�
��1��30��30
��2���⣺��AOM����NOC
=����AOM+��AON��������NOC+��AON��
=90�㩁60��
=30��
���������⣺��1���ߡ�BOC=120�㣬 ���AOC=180�㩁120��=60�㣬
��OMǡ��ƽ�֡�BOC��
���COD=30�㣬��AOD=30�㣮
���Դ��ǣ�30��30��
�����㾫����������Ҫ�����˽ǵ��������ǺͲ��ǵ����������֪ʶ�㣬��Ҫ���ս�֮����Խ��мӼ����㣻һ���ǿ����������ǵĺͻ������ʾ�����ࡢ������ָ�����ǵ�������ϵ���������ǵ�λ���ز�����ȷ�����⣮

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ