Question

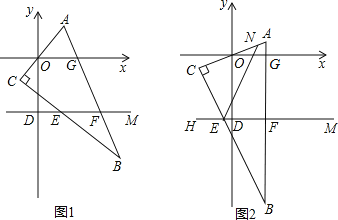
【题目】在平面直角坐标系中，D(0，-3)，M(4，-3)，直角三角形ABC的边与x轴分别交于O、G两点，与直线DM分别交于E、F点．

(1)将直角三角形ABC如图1位置摆放，请写出∠CEF与∠AOG之间的等量关系：______．

(2)将直角三角形ABC如图2位置摆放，N为AC上一点，∠NED+∠CEF=180°，请写出∠NEF与∠AOG之间的等量关系，并说明理由．

Answer 1

【答案】(1)∠CEF=90°+∠AOG；(2)∠AOG+∠NEF=90°．

【解析】

(1)作CP∥x轴，利用D、M点的坐标可得到DM∥x轴，则CP∥DM∥x轴，根据平行线的性质有∠AOG=∠1，∠2+∠CEF=180°，然后利用∠1+∠2=90°得到∠AOG+∠180°-∠CEF=90°，再整理得∠CEF=90°+∠AOG；

(2)作CP∥x轴，则CP∥DM∥x轴，根据平行线的性质得∠AOG=∠1，∠2+∠CEF=180°，由于∠NED+∠CEF=180°，所以∠2=∠NED，然后利用∠1+∠2=90°即可得到∠AOG+∠NEF=90°．

解：(1)∠CEF与∠AOG之间的等量关系为：∠CEF=90°+∠AOG．

作CP∥x轴，如图1，

∵D(0，-3)，M(4，-3)，

∴DM∥x轴，

∴CP∥DM∥x轴，

∴∠AOG=∠1，∠2+∠CEF=180°，

∴∠2=180°-∠CEF，

∵∠1+∠2=90°，

∴∠AOG+∠180°-∠CEF=90°，

∴∠CEF=90°+∠AOG；

故答案为∠CEF=90°+∠AOG；

(2)∠AOG+∠NEF=90°．理由如下：

作CP∥x轴，如图2，

∵CP∥DM∥x轴，

∴∠AOG=∠1，∠2+∠CEF=180°，

而∠NED+∠CEF=180°，

∴∠2=∠NED，

∵∠1+∠2=90°，

∴∠AOG+∠NEF=90°．