题目内容
【题目】如图，已知点E、F在四边形ABCD的对角线延长线上，AE=CF，DE∥BF，∠1=∠2．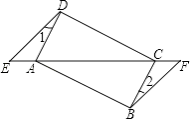
（1）求证：△AED≌△CFB；
（2）若AD⊥CD，四边形ABCD是什么特殊四边形？请说明理由．
【答案】
（1）证明：∵DE∥BF，
∴∠E=∠F，
在△AED和△CFB中，
，
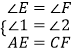∴△AED≌△CFB（AAS）
（2）解：四边形ABCD是矩形．
理由如下：∵△AED≌△CFB，
∴AD=BC，∠DAE=∠BCF，
∴∠DAC=∠BCA，
∴AD∥BC，
∴四边形ABCD是平行四边形，
又∵AD⊥CD，
∴四边形ABCD是矩形．
【解析】(1)利用两直线平行，内错角相等可得一组对应角相等，结合已知条件，运用角角边证得全等；（2）利用（1）的结论，可证得平行四边形，再结合已知条件AD⊥CD，可证得矩形.
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
点睛新教材全能解读系列答案
相关题目
