题目内容
如图,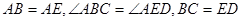 ,点
,点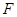 是
是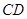 的中点
的中点
(1)请说明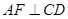 的理由
的理由
(2)连结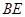 后,还能得出什么新的结论?请写出三个(不要求说明理由)(8分)
后,还能得出什么新的结论?请写出三个(不要求说明理由)(8分)
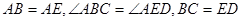 ,点
,点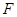 是
是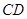 的中点
的中点
(1)请说明
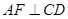 的理由
的理由(2)连结
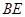 后,还能得出什么新的结论?请写出三个(不要求说明理由)(8分)
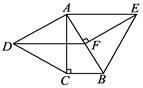
后,还能得出什么新的结论?请写出三个(不要求说明理由)(8分)(1)AF⊥CD.
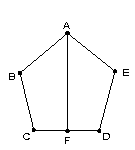
理由:如图,连接AC、AD,
∵AB=AE,∠ABC=∠AED,BC=ED
∴△ABC≌△AED
∴AC=AD,即△ACD是等腰三角形,
∵F是CD的中点
∴AF是等腰△ACD的CD边上的高,即AF⊥CD;
(2)答案不惟一.如:△ABE是等腰三角形,或四边形BCDE是等腰梯形,或∠ABE=∠AEB,或AF垂直平分BE等等.
理由:如图,连接AC、AD,
∵AB=AE,∠ABC=∠AED,BC=ED
∴△ABC≌△AED
∴AC=AD,即△ACD是等腰三角形,
∵F是CD的中点
∴AF是等腰△ACD的CD边上的高,即AF⊥CD;
(2)答案不惟一.如:△ABE是等腰三角形,或四边形BCDE是等腰梯形,或∠ABE=∠AEB,或AF垂直平分BE等等.
1、连接AC、AD,由△ABC≌△AED得AC=AD,再由等腰三角形的“三线合一”即得;
2、由AB=AE得:△ABE是等腰三角形,由等腰三角形的性质可得AF垂直平分BE,由AF垂直平分BE,AF垂直平分CD,可得四边形BCDE是等腰梯形.
2、由AB=AE得:△ABE是等腰三角形,由等腰三角形的性质可得AF垂直平分BE,由AF垂直平分BE,AF垂直平分CD,可得四边形BCDE是等腰梯形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
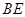 平分
平分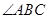 ,交
,交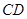 于点
于点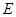 ,点
,点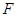 在边
在边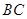 上.
上.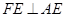 ,那么
,那么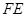 和
和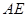 相等吗?证明你的结论.
相等吗?证明你的结论.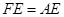 ,那么
,那么
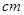 ,高为12
,高为12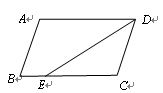
 的边长为
的边长为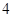 ,
,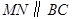 分别交
分别交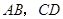 于点
于点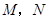 ,在
,在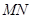 上任取两点
上任取两点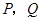 ,那么图中阴影部分的面积是 .
,那么图中阴影部分的面积是 .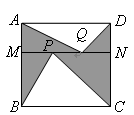
 ABCD中,AD=5cm,AB=3cm。AE平分∠BAD交BC于点E,则CE的长等于 ( )
ABCD中,AD=5cm,AB=3cm。AE平分∠BAD交BC于点E,则CE的长等于 ( )