Question

【题目】已知：Rt△ABC，∠C＝90°．

（1）点E在BC边上，且△ACE的周长为AC＋BC，以线段AE上一点O为圆心的⊙O恰与AB、BC边都相切．请用无刻度的直尺和圆规确定点E、O的位置；

（2）若BC＝8，AC＝4，求⊙O的半径．

Answer 1

【答案】（1）见解析；（2）

【解析】

（1）根据垂直平分线的性质以及角平分线的性质作图即可；

（2）先根据勾股定理得出AB的长，再根据S△ABE＝S△AOB＋S△BOE即可得出⊙O的半径．

（1）如图，点E、O即为所求作点，

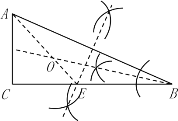
（2）解：设AE＝BE＝x，则CE＝8－x

在Rt△ACE中，42＋（8－x）2＝x2

x＝5

在Rt△ABC中，AB＝＝

∵S△ABE＝S△AOB＋S△BOE

∴×5×4＝×r＋×5r

∴r＝．