Question

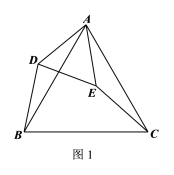
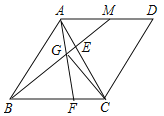
【题目】如图，在菱形ABCD中，∠ABC＝60°，M为AD的中点，连接BM，交AC于E，在CB上取一点F，使得CF＝AE，连接AF，交BM于G，连接CG．

（1）求∠BGF的度数；

（2）求的值；

（3）求证：BG⊥CG．

Answer 1

【答案】（1）60°；（2） ；（3）证明见解析

【解析】

（1）证明△BAE≌△ACF（SAS），推出∠ABE＝∠CAF可得结论．

（2）证明△BAG∽△BMA，推出，推出即可解决问题．

（3）想办法证明△CBG∽△MBC可得结论．

解：（1）∵四边形ABCD是菱形，

∴AB＝BC＝CD＝AD，∠ABC＝∠ADC＝60°，

∴△ABC，△ADC都是等边三角形，

∴AB＝AC，∠BAE＝∠ACF＝60°，

∵AE＝CF，

∴△BAE≌△ACF（SAS），

∴∠ABE＝∠CAF，

∴∠BGF＝∠ABE+∠BAG＝∠CAF+∠BAG＝∠BAC＝60°．

（2）∵∠BAG+∠ABG＝∠ABG+∠CBM＝60°，

∴∠BAG＝∠CBM，

∵AD∥CB，

∴∠AMB＝∠CBM，

∴∠BAG＝∠BMA，

∵∠ABG＝∠ABM，

∴△BAG∽△BMA，

∴，

∴，

∵AM＝MD＝AD＝AB，

∴．

（3）设AM＝DM＝x，连接CM，

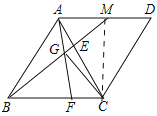
∵△ACD是等边三角形，

∴CM⊥AD，

∴CM＝AM＝，

∵AD∥CB，

∴CM⊥BC，

∴∠BCM＝90°，

∵AD＝BC＝2x，

∴BM＝，

∵△BAG∽△BMA，

∴，

∴，

∴BG＝，

∴，

∵∠CBG＝∠CBM，

∴△CBG∽△MBC，

∴∠BGC＝∠BCM＝90°，

∴BG⊥CG．