题目内容
如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA与⊙O的另一个交点为E,连结AC,CE.

(1)求证:∠B=∠D;
(2)若AB=4,BC-AC=2,求CE的长.

(1)求证:∠B=∠D;
(2)若AB=4,BC-AC=2,求CE的长.
(1)证明见解析;(2)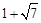 .
.
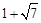 .
.试题分析:(1)由AB为⊙O的直径,易证得AC⊥BD,又由DC=CB,根据线段垂直平分线的性质,可证得AD=AB,即可得:∠B=∠D;
(2)首先设BC=x,则AC=x-2,由在Rt△ABC中,
 ,可得方程:
,可得方程: ,解此方程即可求得CB的长,继而求得CE的长.
,解此方程即可求得CB的长,继而求得CE的长.试题解析:(1)∵AB为⊙O的直径,∴∠ACB="90°." ∴AC⊥BC.
∵DC=CB,∴AD="AB." ∴∠B=∠D.
(2)设BC=x,则AC=x-2,
在Rt△ABC中,
 ,
,∴
 ,解得:
,解得: (舍去).
(舍去).∵∠B=∠E,∠B=∠D,∴∠D=∠E. ∴CD="CE"
∵CD=CB,∴CE=CB=
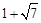 .
.
练习册系列答案
相关题目
 于D,点A是优弧
于D,点A是优弧 上的动点(不与B、C重合),BC=
上的动点(不与B、C重合),BC= ,ED=2.
,ED=2.




 的菱形OABC的顶点A,C,B分别在OD,OE,弧ED上,若把扇形DOE围成一个圆锥,则此圆锥的高为( )
的菱形OABC的顶点A,C,B分别在OD,OE,弧ED上,若把扇形DOE围成一个圆锥,则此圆锥的高为( )




 =
= ,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.给出下列结论:
,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.给出下列结论: ;④S△DEF=
;④S△DEF= .
.




