题目内容
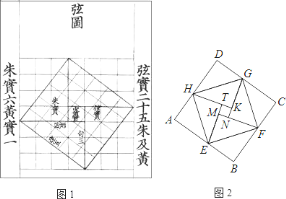
【题目】课间,小聪拿着老师的等腰直角三角板玩,不小心掉到两墙之间(如图),![]() ,
,![]() ,从三角板的刻度可知
,从三角板的刻度可知![]() ,小聪很快就知道了砌墙砖块的厚度的平方(每块砖的厚度相等)为________
,小聪很快就知道了砌墙砖块的厚度的平方(每块砖的厚度相等)为________![]() .
.

【答案】![]()
【解析】
首先证明△ACD≌△CEB(AAS),进而利用勾股定理,在Rt△AFB中,AF2+BF2=AB2,求出即可.
解:过点B作BF⊥AD于点F,
设砌墙砖块的厚度为xcm,则BE=2xcm,则AD=3xcm,
∵∠ACB=90°,
∴∠ACD+∠ECB=90°,
∵∠ECB+∠CBE=90°,
∴∠ACD=∠CBE,
在△ACD和△CEB中,
 ,
,
∴△ACD≌△CEB(AAS),
∴AD=CE,CD=BE,
∴DE=5x,AF=AD-BE=x,
∴在Rt△AFB中,
AF2+BF2=AB2,
∴25x2+x2=400,
解得,x2=![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目
【题目】某校学生会决定从三名学生会干事中选拔一名干事,对甲、乙、丙三名候选人进行了笔试和面试,三人的测试成绩如下表所示:
测试项目 | 测试成绩/分 | ||
甲 | 乙 | 丙 | |
笔试 | 75 | 80 | 90 |
面试 | 93 | 70 | 68 |
根据录用程序,学校组织200名学生采用投票推荐的方式,对三人进行民主测评,三人得票率(没有弃权,每位同学只能推荐1人)如扇形统计图所示,每得一票记1分.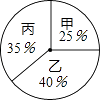
(1)分别计算三人民主评议的得分;
(2)根据实际需要,学校将笔试、面试、民主评议三项得分按4:3:3的比例确定个人成绩,三人中谁的得分最高?