��Ŀ����
����Ŀ���Ķ�������ϣ�
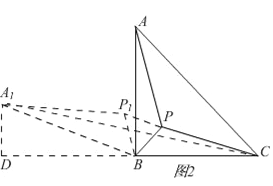
Сΰ��������һ�����⣺��ͼ1���ڡ�ABC�����С�BAC��һ�����Ա仯�Ľǣ��У�AB=2��AC=4����BCΪ����BC���·����ȱߡ�PBC����AP�����ֵ��
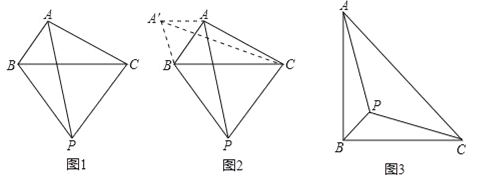
Сΰ������˼���ģ����ñ任�͵ȱ������ν��ߵ�λ��������ϣ����ķ������Ե�BΪ��ת���Ľ���ABP��ʱ����ת60��õ���A��BC������A��A������A����A��C��ʱ������ɽ⣨��ͼ2����
��1������ش�AP�����ֵ�� ��
��2���ο�Сΰͬѧ˼������ķ���������������⣺
��ͼ3������Rt��ABC����AB=4��PΪ��ABC�ڲ�һ�㣬��д����AP+BP+CP����Сֵ���Ľ���˼·��
��ʾ��Ҫ���AP+BP+CP����Сֵ���⣬�ɷ�����Ŀ�������������ѡ�ABP��B����ʱ����ת60���õ���A��BP�䣮
���뻭����ת���ͼ��
����д����AP+BP+CP����Сֵ�Ľ���˼·��������Բ�����
���𰸡���1��6����2������ͼ����������![]() ��˼·��������
��˼·��������
��������
�����������1������ת�õ���A��BC���С�A��BA�ǵȱ������Σ�����A��A��C���㹲��ʱ��A��C=AA��+AC����ɣ�
��2������ת�õ�����PA+PB+PC=P1A1+P1B+PC��ֻ�У�A1��P1��P��C�ĵ㹲��ʱ����P1A+P1B+PC����̣����߶�A1C��̣����ݹ��ɶ��������ɣ�
�����������1���ߡ�ABP��ʱ����ת60��õ���A��BC�����A��BA=60�㣬A��B=AB��AP=A��C
���A��BA�ǵȱ������Σ���A��A=AB=BA��=2���ڡ�AA��C�У�A��C��AA��+AC����AP��6����A��A��C���㹲��ʱ��A��C=AA��+AC����AP=6����AP�����ֵ�ǣ�6��
�ʴ�Ϊ��6��
��2������ת���ͼ����ͼ1��
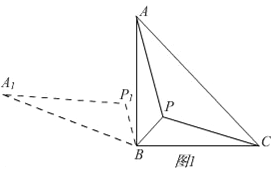
����ͼ2����Rt��ABC�ǵ��������Σ���AB=BC��
��BΪ���ģ�����APB��ʱ����ת60��õ���A1P1B����A1B=AB=BC=4��PA=P1A1��PB=P1B����PA+PB+PC=P1A1+P1B+PC��
�ߵ�A1��P1��P��C�ĵ㹲��ʱ����P1A+P1B+PC����̣����߶�A1C��̣���A1C=PA+PB+PC����A1C���ȼ�Ϊ����
��A1��A1D��CB�ӳ�����D��
�ߡ�A1BA=60�㣨����ת��֪�������A1BD=30�㣮
��A1B=4����A1D=2��BD=![]() ����CD=4+
����CD=4+![]() ��
��
��Rt��A1DC��A1C=![]() =
=![]() =
=![]() ��
��

 ��ѧ����ͬ����ϰϵ�д�
��ѧ����ͬ����ϰϵ�д� ��ǰ�κ�ͬ����ϰϵ�д�
��ǰ�κ�ͬ����ϰϵ�д� ����С��ҵϵ�д�
����С��ҵϵ�д� �Ƹ�С״Ԫ����������ϰ��ϵ�д�
�Ƹ�С״Ԫ����������ϰ��ϵ�д� �ɹ�ѵ���ƻ�ϵ�д�
�ɹ�ѵ���ƻ�ϵ�д� ����ѵ����ֱͨ�п�����ϵ�д�
����ѵ����ֱͨ�п�����ϵ�д�