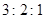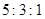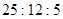题目内容
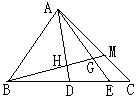
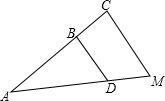
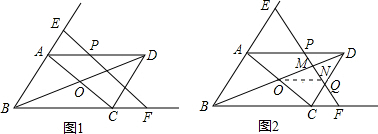
如图,已知?ABCD的对角线交于O点,M为OD的中点,过M的直线分别交AD于CD于P、Q,与BA、BC的延长线于E、F

(1)如图1,若EF∥AC,求证:PE+QF=2PQ;
(2)如图2,若EF与AC不平行,则(1)中的结论是否仍然成立?若成立,加以证明;不成立,请说明理由.

(1)如图1,若EF∥AC,求证:PE+QF=2PQ;
(2)如图2,若EF与AC不平行,则(1)中的结论是否仍然成立?若成立,加以证明;不成立,请说明理由.
(1)如图1,∵MP∥OA,DM=MO,
∴DP=PA.
在?ABCD中,∵AB∥CD,
∴∠EAP=∠QDP,∠AEP=∠DQP.
在△APE与△DPQ中,
,
∴△APE≌△DPQ(AAS),
∴PE=PQ.
同理,QF=PQ,
∴PE+QF=2PQ;
(2)若EF与AC不平行,则(1)中的结论仍然成立.理由如下:
如图2,过O点作ON∥AD交EF于N,则ON是梯形CFPA的中位线,则AP+CF=2ON.
易证△OMN≌△DMP,
∴ON=PD,
∴AP+CF=2PD.
∵CF∥PD,∴
=
,
∵DQ∥AE,∴
=
,
∴
+
=
+
,即
=
=
=2,
∴QF+PE=2PQ.
∴DP=PA.
在?ABCD中,∵AB∥CD,
∴∠EAP=∠QDP,∠AEP=∠DQP.
在△APE与△DPQ中,
|
∴△APE≌△DPQ(AAS),
∴PE=PQ.
同理,QF=PQ,
∴PE+QF=2PQ;

(2)若EF与AC不平行,则(1)中的结论仍然成立.理由如下:
如图2,过O点作ON∥AD交EF于N,则ON是梯形CFPA的中位线,则AP+CF=2ON.
易证△OMN≌△DMP,
∴ON=PD,
∴AP+CF=2PD.
∵CF∥PD,∴
| QF |
| PQ |
| CF |
| PD |
∵DQ∥AE,∴
| PE |
| PQ |
| AP |
| PD |
∴
| QF |
| PQ |
| PE |
| PQ |
| CF |
| PD |
| AP |
| PD |
| QF+PE |
| PQ |
| CF+AP |
| PD |
| 2PD |
| PD |
∴QF+PE=2PQ.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
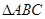 中,
中, 、
、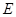 是
是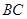 边上的点,
边上的点,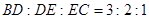 ,
,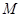 在
在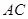
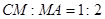 ,
,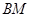 交
交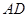 、
、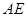 于
于 、
、 ,则
,则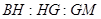 等于 ( )
等于 ( )